Рубрика: Ответы

Итоговая контрольная работа по алгебре за курс 9 класса для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и ОТВЕТЫ. Цитаты из пособия «Алгебра 9 класс Самостоятельные и контрольные работы»  (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях. Код материалов: Ответы на КР-8 Алгебра 9 кл.(угл).

Вернуться к Списку контрольных (в ОГЛАВЛЕНИЕ)

Итоговая контрольная работа
по алгебре в 9 классе (угл.)

Тема: Обобщение и систематизация знаний

КР-8. Вариант 1 (задания)

 

КР-8. Вариант 2 (задания)

 

Ответы на КР-8 Алгебра 9 класс (угл).

ОТВЕТЫ на Вариант 1

№ 1. Постройте график функции f(х) = х² – 6х. Используя график, найдите:
1) область значений функции;
2) промежуток убывания функции;
3) множество решений неравенства f(x) > –8.
ОТВЕТ: 1) E(f) = [–9; +∞);
2) функция убывает при х = (–∞; 3);
3) если f(x) > –8, то х ∈ (–∞; 1) ∪ (5; +∞).

№ 2. Решите неравенство …
ОТВЕТ: х ∈ (–3; –1] ∪ (2; 3)

№ 3. Решите систему уравнений х² – ху = –8, у² – ху = 24.
ОТВЕТ: (4√2; 5√2); (–4√2; –5√2).

№ 4. Двое трактористов, работая вместе, могут вспахать поле за 4 дня. Если первый тракторист вспашет – поля, а затем его заменит второй, то всё поле будет вспахано за 10 дней. За сколько дней может вспахать поле каждый тракторист, работая самостоятельно?
ОТВЕТ: 6 дней, 12 дней.

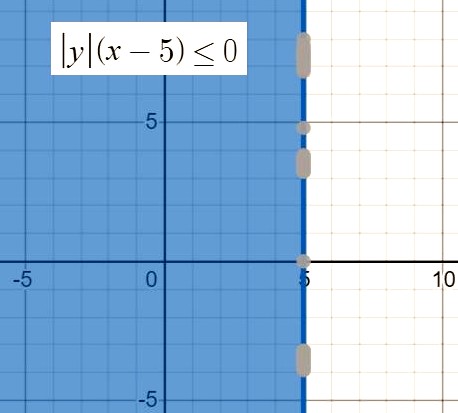
№ 5. Постройте график неравенства |у|(х–5) ≤ 0.
ОТВЕТ:

№ 6. На четырёх карточках записаны числа 5, 6, 7 и 8. Какова вероятность того, что сумма чисел, записанных на двух наугад выбранных карточках, будет нечётным числом?
ОТВЕТ: Р = 2/3.

№ 7. Докажите, что если а > 0 и b > 0, то (9 + 1/a)(25 + 1/b)(1 + 4аb) ≥ 240.
ОТВЕТ: 2 • √(9/a) • 2 • √(25/b) • 2 • √(4ab)= 8 • 3 • 5 • 2 = 240.

№ 8. При каких значениях параметра а неравенство (а – 4)х² + (8 – 2а)х + 5 > 0 выполняется при всех действительных значениях х?
ОТВЕТ: a ∈ (4; 9).

 

ОТВЕТЫ на Вариант 2

№ 1. Постройте график функции f(x) = –x² + 6х. Используя график, найдите:
1) область значений функции;
2) промежуток убывания функции;
3) множество решений неравенства f(x) < 5.
ОТВЕТ: 1) E(f) = (–∞; 9];
2) функция убывает при х = (3; +∞);
3) если f(x) < 5, то х ∈ (–∞; 1) ∪ (5; +∞).

№ 2. Решите неравенство (x² + 6х + 8)/(x² – 4х + 3) ≤ 0.
ОТВЕТ: х ∈ [–5; –1] ∪ [1; 3)

№ 3. Решите систему уравнений
{ х² + xy = 6,
{ xy + y² = 3.
ОТВЕТ: (2; 1); (–2; –1).

№ 4. Две строительные бригады, работая вместе, могут заасфальтировать участок трассы за 20 дней. Если первая бригада заасфальтирует 1/6 часть участка трассы, а затем её заменит вторая, то весь участок трассы будет заасфальтирован за 35 дней. За сколько дней каждая из бригад может заасфальтировать этот участок трассы, работая самостоятельно?
ОТВЕТ: Два решения. Если 1–я бригада за 28 дней, то вторая за 70 дней. А если 1–я бригада за 30 дней, то 2–я за 60 дней.

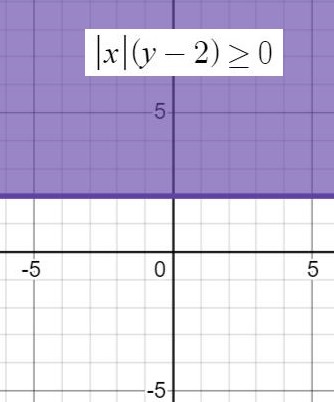
№ 5. Постройте график неравенства |х|(у–2) ≥ 0.
ОТВЕТ:

№ 6. На четырёх карточках записаны числа 3, 4, 5 и 6. Какова вероятность того, что произведение чисел, записанных на двух наугад выбранных карточках, будет кратным числу 3?
ОТВЕТ: Р = 5/6.

№ 7. Докажите, что если а > 0 и b > 0, то (1 + 1/a)(4 + 1/b)(1 + 16ab) ≥ 64.
ОТВЕТ: 2 • √(1/a) • 2 • √(4/b) • 2 • √(16ab)= 8 • 2 • 1 • 4 = 64

№ 8. При каких значениях параметра а неравенство (а – 6)x² + (12 – 2а)х + 7 > 0 выполняется при всех действительных значениях х?
ОТВЕТ: а ∈ (–∞; –1) ∪ (6; +∞).

 

---

ГДЗ Алгебра 9 класс. Итоговая контрольная работа по алгебре за курс 9 класса для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и ОТВЕТЫ. Цитаты из пособия «Алгебра 9 класс Самостоятельные и контрольные работы»  (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях. Код материалов: Ответы на КР-8 Алгебра 9 кл.(угл).

Вернуться к Списку контрольных (в ОГЛАВЛЕНИЕ)

 

Алгебра 9 класс. Контрольная работа КР-7 «Числовые последовательности» для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и ОТВЕТЫ. Цитаты из пособия «Алгебра 9 класс Самостоятельные и контрольные работы»  (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях. Код материалов: Ответы на КР-7 Алгебра 9 кл.(угл).

Вернуться к Списку контрольных (в ОГЛАВЛЕНИЕ)

Контрольная работа № 7
по алгебре в 9 классе (угл.)

Тема: Числовые последовательности

КР-7. Вариант 1 (задания)

 

КР-7. Вариант 2 (задания)

 

Ответы на КР-7 Алгебра 9 класс (угл).

ОТВЕТЫ на Вариант 1

№ 1. Найдите первый отрицательный член арифметической прогрессии 6,3; 5,9; 5,5; … .
ОТВЕТ: а₁₇ = –0,1.

№ 2. Первый и четвёртый члены геометрической прогрессии соответственно равны 2,5 и 20. Найдите сумму восьми первых членов этой прогрессии.
ОТВЕТ: S₈ = 637,5

№ 3. При каком значении х значения выражений 2х + 6, х + 7 и х + 4 будут последовательными членами геометрической прогрессии? Найдите члены этой прогрессии.
ОТВЕТ: x = –5; члены этой прогрессии –4; 2; –1.

№ 4. Сумма бесконечной геометрической прогрессии равна 27, а сумма трёх её первых членов равна 35. Найдите первый член и знаменатель прогрессии.
ОТВЕТ: b₁ = 9; q = 2/3.

№ 5. Найдите сумму всех натуральных чисел, кратных 6, которые больше 100 и меньше 200.
ОТВЕТ: 2550.

№ 6. Последовательность задана рекуррентно: а₁ = 4, а₂ = 10, а_n+2 = 4а_n+1 – 3а_n. Докажите, что а_n = 3ⁿ + 1.
ОТВЕТ: a₃ = 4a₂ – 3a₁ = 28.
a₁ = 4 = 3¹ + 1; a₂ = 10 = 3² + 1; a₃ = 28 = 3³ + 1 => a_n = 3ⁿ + 1.

№ 7. Найдите сумму 1/(√1+√6) + 1/(√6+√11) + 1/(√11+√16) + … + 1/(√116+√121).
ОТВЕТ: 1/(√(5n + 1) + √(5(n+1) + 1)), n ≤ 23, n ∈ N.

 

ОТВЕТЫ на Вариант 2

№ 1. Найдите первый положительный член арифметической прогрессии –8,1; –7,9; –7,7; … .
ОТВЕТ: a₂₃ = 0,7.

№ 2. Первый и шестой члены геометрической прогрессии соответственно равны 2 и –64. Найдите сумму десяти первых членов этой прогрессии.
ОТВЕТ: S₁₀ = –682.

№ 3. При каком значении х значения выражений х + 1, х + 5 и 2х + 4 будут последовательными членами геометрической прогрессии? Найдите члены этой прогрессии.
ОТВЕТ: x = 7; члены этой прогрессии 8; 12; 18.

№ 4. Сумма бесконечной геометрической прогрессии равна 162, а сумма трёх её первых членов равна 156. Найдите первый член и знаменатель прогрессии.
ОТВЕТ: b₁ = 216; q = 1/3.

№ 5. Найдите сумму всех натуральных чисел, кратных 8, которые больше 50 и меньше 180.
ОТВЕТ: S₁₆ = 1856.

№ 6. Последовательность задана рекуррентно: а₁ =3, а₂ = 5, а_n+2 = 3а_n+1 – 2а_n. Докажите, что а_n = 2ⁿ + 1.
ОТВЕТ: a₃ = 3a₂ – 2a₁ = 9.
a₁ = 3 = 2¹ + 1; a₂ = 5 = 2² + 1; a₃ = 9 = 2³ + 1 => a_n = 2ⁿ + 1.

№ 7. Найдите сумму 1/(√1+√8) + 1/(√8+√15) + 1/(√15+√22) + … + 1/(√162+√169).
ОТВЕТ: 1/(√(7n + 1) + √(7(n+1) + 1)), n ≤ 23, n ∈ N.

 

---

ГДЗ Алгебра 9 класс. Контрольная работа № 7 «Числовые последовательности» для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и ОТВЕТЫ. Цитаты из пособия «Алгебра 9 класс Самостоятельные и контрольные работы»  (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях. Код материалов: Ответы на КР-7 Алгебра 9 кл.(угл).

Вернуться к Списку контрольных (в ОГЛАВЛЕНИЕ)

 

Алгебра 9 класс. Контрольная работа КР-6 Элементы комбинаторики и теории вероятностей для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и ОТВЕТЫ. Цитаты из пособия «Алгебра 9 класс Самостоятельные и контрольные работы»  (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях. Код материалов: Ответы на КР-6 Алгебра 9 кл.(угл).

Вернуться к Списку контрольных (в ОГЛАВЛЕНИЕ)

Контрольная работа № 6
по алгебре в 9 классе (угл.)

Тема: Элементы комбинаторики и теории вероятностей

КР-6. Вариант 1 (задания)

 

КР-6. Вариант 2 (задания)

 

Ответы на КР-6 Алгебра 9 класс (угл).

ОТВЕТЫ на Вариант 1

№ 1. Найдите значение выражения: 1) (3P₁₂ – P₁₁)/(7P₁₀); 2) (A₅²)/(C₆³).
ОТВЕТ: 1) 55; 2) 1.

№ 2. В коробке лежат шары, из которых девять — синие, а остальные — зелёные. Сколько в коробке зелёных шаров, если вероятность того, что выбранный наугад шар окажется зелёным, равна 4/7?
ОТВЕТ: 12 зеленых шаров.

№ 3. Сколько чётных четырёхзначных чисел, все цифры которых различны, можно записать с помощью цифр 2, 3, 4, 7 и 9?
ОТВЕТ: 24 числа.

№ 4. Найдите все натуральные значения n, при которых выполняется неравенство 2ⁿ ≥ 3n – 1.
Указание к решению: Чтобы решить это неравенство, надо сначала решить соответствующее уравнение: 2ⁿ = 3n – 1.
ОТВЕТ: n ∈ {1} ∪ [3;+∞), n ∈ N.

Геометрия 7 Контрольная 2 В34 (Мерзляк). Контрольная работа по геометрии в 7 классе «Треугольники» (варианты 3, 4) для УМК Мерзляк, Полонский, Якир в 4-х вариантах. Методическое пособие + Ответы и решения.

Варианты 1 и 2 смотрите тут: К-2 Варианты 1-2

Вернуться к списку работ (в Оглавление)

Геометрия 7 класс (УМК Мерзляк)

Контрольная работа № 2 (В-3, В-4)

Тема контрольной: Треугольники.

К-2 Варианты 3, 4 (задания)

 

Решения и ОТВЕТЫ на Вариант 3

№ 1. Докажите равенство треугольников ABM и CDM (рис. 46), если AM = CM и ∠BAM = ∠DCM.

Дано: ∆АВМ и ∆СDM, АМ=СМ, ∠ВАМ=∠DCM.
Доказать: ∆АВМ = ∆СDM.
Доказательство: так как 1) ∠ВАМ=∠DCM по условию,
2) АМ = СМ по условию,
3) ∠АМВ=∠CMD как вертикальные, то
∆АВМ = ∆СDM по 2-му признаку равенства треугольников (Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника).

№ 2. Найдите стороны равнобедренного треугольника, если его периметр равен 49 см, а основание на 7 см больше боковой стороны.
Дано: ∆ABC — равнобедренный; Рabc = 49 см; основание на 7см больше боковой стороны.
Найти: АВ, ВС, АС – ?
Решение: Рabc = АВ + ВС + АС.
Пусть АВ = ВС = x, тогда АС = х + 7;
49 = х + х + х + 7  =>  42 = 3х  =>  х = 14.
AB = BC = 14 (см);  АС = х + 7 =21 (см).
ОТВЕТ: 21 см, 14 см, 14 см.

№ 3. На боковых сторонах AB и BC равнобедренного треугольника ABC отметили соответственно точки M и K так, что BM = BK. Докажите, что ∠BAK = ∠BCM.

Доказательство: Рассмотрим ∆АВК и ∆СВМ. Так как
1) ∠В – общий угол для этих треугольников,
2) АВ = СВ, так как треугольник АВС – равнобедренный по условию,
3) ВМ = ВК — по условию задачи.
Следовательно, ∆АВК и ∆СВМ равны по двум сторонам и углу между ними (1-й признак рав-ва ∆). В равных треугольника напротив равных сторон лежат равные углы. Следовательно, ∠ВАК = ∠ВСМ, что и требовалось доказать.

№ 4. Известно, что CK = DK и ∠CKP = ∠DKP (рис. 47). Докажите, что ∠MCP = ∠MDP.

Дано: CK = DK, ∠CKP = ∠DKP.
Доказать: ∠MCP = ∠MDP.
Доказательство: 1) CK = DK (по условию), ∠CKP = ∠DKP (по условию), PK – общая, следовательно ΔCPK = ΔDPK (1–й признак, по 2-м сторонам и углу между ними),
2) CK = DK (по условию), ∠CKP = ∠DKP (по условию), МK – общая, следовательно ΔMCK = ΔMDK (1–й признак, по 2-м сторонам и углу между ними),
3) так как ΔCPK = ΔDPK, то CP = PD, а так как ΔMCK = ΔMDK, то CM = MD, MP – общая. Следовательно, ΔMCP = ΔMDP (3–й признак, по трем сторонам).
4) из равенства ΔMCP = ΔMDP следует, что ∠MCP = ∠MDP.

№ 5. Серединный перпендикуляр стороны AC треугольника ABC пересекает его сторону BC в точке D. Найдите периметр треугольника ABD, если AB = 10 см, BC = 15 см.

Решение: Рассмотрим треугольник ΔACD. Так как DO серединный перпендикуляр, то АO = СO. Так как DO перпендикуляр к АС, тогда ДO высота и медиана треугольника АСD, а следовательно АСD равнобедренный треугольник, АD = СD. Периметр треугольника АВD равен: Р_ABD = АВ + ВD + АD = АВ + СD + ВD = АВ + ВС = 10 + 15 = 25 см.
ОТВЕТ: P_ABD = 25 см.

---

Варианты 1 и 2 смотрите тут: К-2 Варианты 1-2

Геометрия 7 Контрольная 2 В34

Решения и ОТВЕТЫ на Вариант 4

№ 1. Докажите равенство треугольников ABD и ACD (рис. 48), если AB = AC и BD = CD.

Дано: ∆АВD и ∆AСD, АB = AС, BD = CD.
Доказать: ∆АВD = ∆AСD.
Доказательство: так как 1) АB = AС по условию,
2) BD = CD по условию,
3) АD – общая, то
∆АВD = ∆AСD по 3-му признаку равенства треугольников (по трем сторонам).

№ 2. Найдите стороны равнобедренного треугольника, если его периметр равен 40 см, а боковая сторона на 2 см больше основания.
Решение: Пусть основание равно x см, тогда боковая сторона равна (x+2) см. Две боковые стороны равны (по определению равнобедренного треугольника). Тогда периметр треугольника
Р = x + (x+2) + (x+2) = 40;
3x + 4 = 40  =>  3x = 36  =>  x = 36/3 = 12 (см).
Следовательно, основание = 12см;
боковая сторона = х+2 = 12+2 = 14 (см).
ОТВЕТ: 12 см, 14 см, 14 см.

№ 3. На основании AC равнобедренного треугольника ABC отметили точки D и E так, что AD = CE, точка D лежит между точками A и E. Докажите, что ∠ABD = ∠ CBE.
Доказательство: ΔABC — равнобедренный, поэтому AB = CB (как боковые стороны) и ∠BAC = ∠BCD (как углы при основании).
ΔABD = ΔCBE по двум сторонам и углу между ними (AD = CE; AB = CB; ∠BAD = ∠BCE ⇒ 1–й признак рав-ва);
В равных треугольника напротив равных сторон лежат равные углы, поэтому ∠ABD=∠CBE, что и требовалось доказать.

№ 4. Известно, что ∠BST = ∠AST и ∠STB = ∠STA (рис. 49). Докажите, что BK = AK.

Доказательство: 1) ΔSBK = ΔSAT по стороне и двум прилежим к ней углам (ST – общая сторона; ∠BST = ∠AST; ∠STB = ∠STA ⇒ 2-й признак), поэтому BT = AT.
2) ΔBKT = ΔAKT по двум сторонам и углу между ними (BT = AT; KT – общая сторона; ∠ATK = ∠BTK ⇒ 1-й признак), поэтому AK = BK, что и требовалось доказать.

№ 5. Прямая, проведённая через вершину A треугольника ABC, перпендикуляр на его медиане CM и делит её пополам. Найдите сторону AC, если AB = 18 см.
Решение: Обозначим точку пересечения прямой, проходящей через точку А, перпендикулярно CM, и прямой CM, точкой H.
Рассмотрим ΔCAM:
MH = HC ⇒ AH – медиана;
AH⊥MC ⇒ AH – высота;
ΔCAM – равнобедренный (MC – основание), поскольку AH – высота и медиана;
Тогда AC = AM, как боковые стороны равнобедренного треугольника.
AM = BM, поскольку CM — медиана ΔABC проведённая из вершины C;
AM = AB/2 = 18 : 2 = 9 (см); AC = AM = 9 (см).
ОТВЕТ: АС = 9 см.

 

---

Вы смотрели: Геометрия 7 Контрольная 2 В34 (Мерзляк). Контрольная работа по геометрии в 7 классе «Треугольники» для УМК Мерзляк, Полонский, Якир (варианты 3, 4).

Варианты 1 и 2 смотрите тут: К-2 Варианты 1-2

Смотреть аналогичную контрольную № 2 из Дидактички (2 варианта)

Вернуться к Списку контрольных из Методички (4 варианта)

Справочный материал:

(с) Цитаты из пособия «Геометрия 7 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Контрольно-измерительные материалы: Контрольная работа № 2 по геометрии 9 класс с ответами «Метод координат» (составитель вопросов — А.Н. Рурукин). Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения, а также для дистанционного обучения в период невозможности посещения образовательного учреждения. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 9 КИМ Контрольная 2 (2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Геометрия 9 класс
Контрольная работа № 2

Тема учебника: Метод координат

 

ОТВЕТЫ на Вариант 1

№ 1. Установите связь между векторами m = –38а + 39b и n = 3 (2/5 • а – 1/3 • b) + 4 (1/3 • а – 2/5 • b).
ОТВЕТ: m = –15n.

№ 2. Векторы m = 2а – 3b и n = 3а + 2b разложены по неколлинеарным векторам а и b. Разложите векторы а и b по векторам m и n.
ОТВЕТ: a = 2/13 • m + 3/13 • n и b = –3/13 • m + 2/13 • n.

№ 3. Четырехугольник имеет вершины с координатами A (1; 1), B (3; 5), C (9; –1), D (7; –5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
ОТВЕТ: Параллелограмм, AC = 2√17 и BD = 2√29.

№ 4. Напишите уравнение окружности с центром в точке C (–3; 1), проходящей через точку A (2; 3).
ОТВЕТ: (x + 3)² + (y – 1)² = 29.

№ 5. Прямая l проходит через точки A (–3; 1) и B (1; –7). Напишите уравнение прямой m, проходящей через точку C (5; 6) и перпендикулярной прямой l.
ОТВЕТ: x – 2y + 17.

 

ОТВЕТЫ на Вариант 2

№ 1. Установите связь между векторами m = –37а + 10b и n = 5 (3/4 • а + 1/3 • b) – 2 (1/3 • а + 5/4 • b).
ОТВЕТ: m = –12n.

№ 2. Векторы m = 3а – 2b и n = 2а + 3b разложены по неколлинеарным векторам а и b. Разложите векторы а и b по векторам m и n.
ОТВЕТ: a = 3/13 • m + 2/13 • n и b = –2/13 • m + 3/13 • n.

№ 3. Четырехугольник имеет вершины с координатами A (–6; 1), B (2; 5), C (4; –1), D (–4; –5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
ОТВЕТ: Параллелограмм, AC = 2√26 и BD = 2√34.

№ 4. Напишите уравнение окружности с центром в точке C (2; –3), проходящей через точку A (–1; –2).
ОТВЕТ: (x – 2)² + (y + 3)² = 10.

№ 5. Прямая l проходит через точки A (2; –1) и B (–3; 9). Напишите уравнение прямой m, проходящей через точку C (3; 10) и перпендикулярной прямой l.
ОТВЕТ: x – 2y + 17 = 0.

 

Ответы в графическом виде:

 

---

Вы смотрели: Контрольная работа № 2 по геометрии 9 класс с ответами «Метод координат». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 9 КИМ Контрольная 2 (2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Контрольно-измерительные материалы: Контрольная работа № 1 по геометрии 9 класс с ответами «Векторы» (составитель вопросов — А.Н. Рурукин). Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения, а также для дистанционного обучения в период невозможности посещения образовательного учреждения. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 9 КИМ Контрольная 1 (2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Геометрия 9 класс
Контрольная работа № 1

Тема учебника: Векторы

 

ОТВЕТЫ на Вариант 1

№ 1. ABCD – параллелограмм, AB = a, AD = b, K ∈ BC, L ∈ AD, BK : KC = 2 : 3, AL : LD = 3 : 2. Найдите разложение вектора KL по неколлинеарным векторам а и b.
ОТВЕТ: 1/5 • b – a.

№ 2. Дана трапеция ABCD с основаниями AD = 20 и BC = 8, О – точка пересечения диагоналей. Разложите вектор DO по векторам AD = а и AB = b.
ОТВЕТ: –5/7 • a + 5/7 • b.

№ 3. Диагонали ромба AC = a, BD = b. Точка K ∈ BD и BK : KD = 1 : 3. Найдите величину |AK|.
ОТВЕТ: 1/4 • √[4a² + b²].

№ 4. В равнобедренной трапеции острый угол равен 60°, боковая сторона равна 12 см, большее основание равно 30 см. Найдите среднюю линию трапеции.
ОТВЕТ: 24 см.

№ 5. В прямоугольнике ABCD известно, что AD = a, DC = b, О – точка пересечения диагоналей. Найдите величину |AB + DO – OB + OC + CD|.
ОТВЕТ: 1/2 • √[a² + b²].

 

ОТВЕТЫ на Вариант 2

№ 1. ABCD – параллелограмм, AD = a, AB = b, K ∈ BC, L ∈ AD, BK : KC = 3 : 4, AL : LD = 4 : 3. Найдите разложение вектора KL по неколлинеарным векторам a и b.
ОТВЕТ: 1/7 • a – b.

№ 2. Дана трапеция ABCD с основаниями AD = 15 и BC = 10, О – точка пересечения диагоналей. Разложите вектор BO по векторам AD = а и AB = b.
ОТВЕТ: 2/5 • a – 2/5 • b.

№ 3. Диагонали ромба AC = a, BD = b. Точка K ∈ AC и AK : KC = 2 : 3. Найдите величину |DK| .
ОТВЕТ: 1/10 • √[a² + 25b²].

№ 4. В равнобедренной трапеции острый угол равен 60°, боковая сторона равна 10 см, меньшее основание равно 14 см. Найдите среднюю линию трапеции.
ОТВЕТ: 19 см.

№ 5. В прямоугольнике ABCD известно, что AB = a, BC = b, О – точка пересечения диагоналей. Найдите величину |AO – BC + OD – OB + DC|.
ОТВЕТ: 1/2 • √[a² + b²].

 

Ответы в графическом виде:

 

---

Вы смотрели: Контрольная работа № 1 по геометрии 9 класс с ответами «Векторы». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 9 КИМ Контрольная 1 (2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Контрольно-измерительные материалы: Итоговая контрольная работа по геометрии 8 класс с ответами (составитель вопросов — Н.Ф.Гаврилова). Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения, а также для дистанционного обучения в период невозможности посещения образовательного учреждения. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 6 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Геометрия 8 класс
Итоговая контрольная работа

 

ОТВЕТЫ на Вариант 1

№ 1. Боковая сторона равнобедренного треугольника равна 10 см, а его основание – 12 см. Найдите его площадь.
ОТВЕТ: 48 см².

№ 2. Диагонали ромба равны 8 см и 6 см. Найдите периметр и площадь ромба.
ОТВЕТ: 20 см; 24 см².

№ 3. В трапеции АВСD углы А и В прямые. Диагональ АС – биссектриса угла А и равна 6 см. Найдите площадь трапеции, если угол СDА = 60°.
ОТВЕТ: (18 + 3√3) см².

№ 4. В окружности проведены две хорды АВ и СD, пересекающиеся в точке К, КС = 6 см, АК = 8 см, ВК + DК = 21 см. Найдите длины ВК и DК.
ОТВЕТ: 9 см;12 см.

№ 5. * Квадрат со стороной 8 см описан около окружности. Найдите площадь прямоугольного треугольника с острым углом 30°, вписанного в данную окружность.
ОТВЕТ: 8√3 см².

---

 

ОТВЕТЫ на Вариант 2

№ 1. Боковая сторона равнобедренного треугольника равна 13 см, а его медиана, проведенная к основанию, – 5 см. Найдите площадь и периметр треугольника.
ОТВЕТ: 60 см²; 50 см.

№ 2. Биссектриса угла А параллелограмма АВСD делит сторону ВС на отрезки ВК и КС, равные соответственно 8 см и 4 см. Найдите периметр параллелограмма.
ОТВЕТ: 40 см.

№ 3. В равнобедренной трапеции АВСD диагональ АС перпендикулярна боковой стороне СD. Найдите площадь трапеции, если угол САD = 30°, АD = 12 см.
ОТВЕТ: 27√3 см².

№ 4. В окружности проведены две хорды АВ и СD, пересекающиеся в точке М, МВ = 10 см, АМ = 12 см, DС = 23 см. Найдите длины СМ и DМ.
ОТВЕТ: 8 см; 15 см.

№ 5. * Равнобедренный прямоугольный треугольник с катетом 4 см вписан в окружность. Найдите площадь квадрата, описанного около этой окружности.
ОТВЕТ: 32 см².

 

Другие варианты итоговой контрольной работы:

УМК Атанасян — Гаврилова: Поурочные разработки (2 варианта)

УМК Атанасян — Иченская: Самостоятельные и контрольные (2 варианта)

 

---

Вы смотрели: Итоговая контрольная работа по геометрии 8 класс с ответами. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 6 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Контрольно-измерительные материалы: Контрольная работа № 5 по геометрии 8 класс с ответами «Окружность» (составитель вопросов — Н.Ф.Гаврилова). Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения, а также для дистанционного обучения в период невозможности посещения образовательного учреждения. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 5 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Геометрия 8 класс
Контрольная работа № 5

Тема учебника: Окружность

 

ОТВЕТЫ на Вариант 1

№ 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см, 4 см и 5 см. Найдите периметр треугольника.
ОТВЕТ: 24 см.

№ 2. Точки А и В делят окружность с центром О на дуги АМВ и АСВ так, что дуга АСВ на 60° меньше дуги АМВ, АМ – диаметр окружности. Найдите величины углов АМВ, АВМ, АСВ.
ОТВЕТ: ∠AMB = 75°; ∠АВМ = 90°; ∠АСВ = 105°.

№ 3. Хорды МЕ и РК пересекаются в точке А так, что МА = 3 см, ЕА = 16 см, РА : КА = 1 : 3. Найдите величину хорды РК и наименьшее значение радиуса этой окружности.
ОТВЕТ: РК = 16 см, наименьшее значение радиуса данной окружности 9,5 см.

№ 4. * В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию, – 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
ОТВЕТ: 3 см; 6,25 см.

---

 

ОТВЕТЫ на Вариант 2

№ 1. В прямоугольный треугольник вписана окружность радиуса 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см.
ОТВЕТ: 6 см; 8 см; 10 см.

№ 2. Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 100° меньше дуги ЕАН, АЕ – диаметр окружности. Найдите величины углов ЕКА, ЕАН, ЕКН.
ОТВЕТ: ∠EKA = 90°; ∠EAH = 65°; ∠EKH = 115°.

№ 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ = 3 см, ВЕ = 36 см, СЕ : DЕ = 3 : 4. Найдите величину хорды СD и наименьшее значение радиуса этой окружности.
ОТВЕТ: CD = 21 см, наименьшее значение радиуса данной окружности 19,5 см.

№ 4. * В равнобедренном треугольнике основание равно 10 см, а высота, проведенная к нему, – 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
ОТВЕТ: 3 ¹/₃ см; 7 ¹/₂₄ см.

 

Другие варианты контрольной работы по теме «Окружность» из пособий:

УМК Атанасян — Гаврилова: Поурочные разработки (3 уровня сложности, 2 варианта)

УМК Атанасян — Иченская: Самостоятельные и контрольные (2 варианта)

 

---

Вы смотрели: Контрольная работа № 5 по геометрии 8 класс с ответами «Окружность». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 5 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Контрольно-измерительные материалы: Контрольная работа № 4 по геометрии 8 класс с ответами «Применение подобия треугольников» (составитель вопросов — Н.Ф.Гаврилова). Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения, а также для дистанционного обучения в период невозможности посещения образовательного учреждения. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 4 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Геометрия 8 класс
Контрольная работа № 4

Тема учебника: Применение подобия треугольников

 

ОТВЕТЫ на Вариант 1

№ 1. На стороне ВС треугольника АВС выбрана точка D так, что ВD : DС = 3 : 2, точка К – середина отрезка АВ, точка Е – середина отрезка АD, КЕ = 6 см, ∠АDС = 100°. Найдите длину стороны ВС и величину угла АЕК.
ОТВЕТ: 20 см; 80°.

№ 2. В прямоугольном треугольнике АВС угол С прямой, АС = 4 см, СВ = 4√3 см, СМ – медиана. Найдите величину угла ВСМ.
ОТВЕТ: 30°.

№ 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен а. Найдите площадь и периметр трапеции.
ОТВЕТ: S = 20 tg a; Р = 20 + 4/cos a.

№ 4. В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА = 13 см, ОВ = 10 см.
ОТВЕТ: 180 см².

№ 5. * В трапеции АВСD (ВС || АD) сторона АВ перпендикулярна диагонали ВD, ВD = 2√5, АD = 2√10, СЕ – высота треугольника ВСD, а тангенс угла ЕСD равен 3. Найдите величину ВЕ.
ОТВЕТ: √5/2.

---

 

ОТВЕТЫ на Вариант 2

№ 1. На стороне АМ треугольника АВМ выбрана точка Н так, что АН : НМ = 4 : 7, точка С – середина отрезка АВ, точка О – середина отрезка ВН, АМ = 22 см, ∠ВОС = 105°. Найдите длину СО и величину угла ВНМ.
ОТВЕТ: 4 см; 75°.

№ 2. В прямоугольном треугольнике MNК угол К прямой, КМ = 6 см, NК = 6√3 см, КD – медиана. Найдите величину угла KDN.
ОТВЕТ: 120°.

№ 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание – 10 см, а меньший угол равен а. Найдите периметр и площадь трапеции.
ОТВЕТ: S = 12 sin a (5 + 3 cos a); Р = 32 + 12 cos a.

№ 4. В прямоугольном треугольнике АВС с прямым углом С медианы пересекаются в точке О. Найдите гипотенузу треугольника АВС, если ВС = 12 см, ОВ = 10 см.
ОТВЕТ: 6√13 см.

№ 5. * В трапеции АВСD сторона АВ перпендикулярна диагонали АС, АС = 6√2, ВС = 12, DЕ – высота треугольника АСD, а тангенс угла АСD равен 2. Найдите величину СЕ.
ОТВЕТ: 2√2.

 

Другие варианты контрольной работы по теме «Применение подобия треугольников» из пособий:

УМК Атанасян — Гаврилова: Поурочные разработки (3 уровня сложности, 2 варианта)

УМК Атанасян — Иченская: Самостоятельные и контрольные (2 варианта)

 

---

Вы смотрели: Контрольная работа № 4 по геометрии 8 класс с ответами «Применение подобия треугольников». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 4 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Контрольно-измерительные материалы: Контрольная работа № 3 по геометрии 8 класс с ответами «Признаки подобия треугольников» (составитель вопросов — Н.Ф.Гаврилова). Цитаты из пособия использованы в учебных целях для семейного и домашнего обучения, а также для дистанционного обучения в период невозможности посещения образовательного учреждения. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 3 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)

 

Геометрия 8 класс
Контрольная работа № 3

Тема учебника: Признаки подобия треугольников

 

ОТВЕТЫ на Вариант 1

№ 1. Отрезки АВ и СD пересекаются в точке О, АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, ОD = 6,3 см. Докажите, что АС || ВD. Найдите: а) DВ : АС; б) отношение периметров и площадей треугольников АОС и DВО.
ОТВЕТ: а) 3 : 4; б) 4 : 3; 16 : 9.

№ 2. Диагонали ромба АВСD пересекаются в точке О, AC = 16 см. На стороне АВ взята точка К так, что прямая ОК перпендикулярна АВ и ОК = 4√3 см. Найдите сторону ромба и вторую диагональ.
ОТВЕТ: 16 см; 16√3 см.

№ 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция.
Указание: использовать подобие треугольников ABD и BDC для доказательства параллельности сторон AB и DC; по условию АB ≠ CD.

№ 4. * В равнобедренном треугольнике MNК с основанием МК, равным 10 см, MN = NК = 20 см. На стороне NК лежит точка А так, что АК : АN = 1 : 3. Найдите длину АМ.
ОТВЕТ: 10 см.

---

 

ОТВЕТЫ на Вариант 2

№ 1. На одной стороне угла В отмечены точки А и D, на другой – Е и С так, что В–D–А и В–Е–С, ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. Докажите, что АС || ЕD. Найдите: а) DЕ : АС; б) отношение периметров и площадей треугольников АВС и DВЕ.
ОТВЕТ: а) 1 : 3; б) 3 : 1; 9 : 1.

№ 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что прямая ОК перпендикулярна АВ и АК = 2 см, ВК = 8 см. Найдите диагонали ромба.
ОТВЕТ: 4√5 см; 8√5 см.

№ 3. В выпуклом четырехугольнике АВСD АВ = 6 см, ВС = 9 см, СD = 10 см, АD = 25 см, АС = 15 см. Докажите, что АВСD – трапеция.
Указание: использовать подобие треугольников АВС и DCA для доказательства параллельности сторон АD и ВС; по условию АD ≠ BC.

№ 4. * В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС лежит точка Н так, что ВН : НС = 3 : 1. Найдите длину АН.
ОТВЕТ: 20 см.

 

Другие варианты контрольной работы по теме «Признаки подобия треугольников» из пособий:

УМК Атанасян — Гаврилова: Поурочные разработки (3 уровня сложности, 2 варианта)

УМК Атанасян — Иченская: Самостоятельные и контрольные (2 варианта)

 

---

Вы смотрели: Контрольная работа № 3 по геометрии 8 класс с ответами «Признаки подобия треугольников». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Код материалов: Геометрия 8 КИМ Контрольная 3 (по 2 варианта).

Вернуться к списку работ (в ОГЛАВЛЕНИЕ)