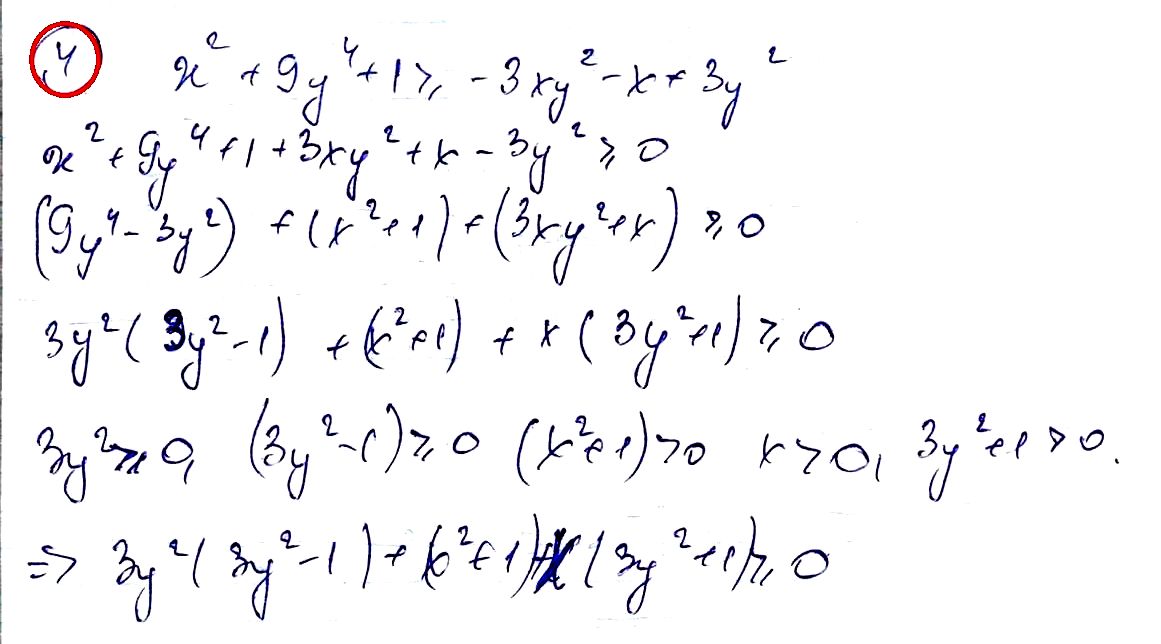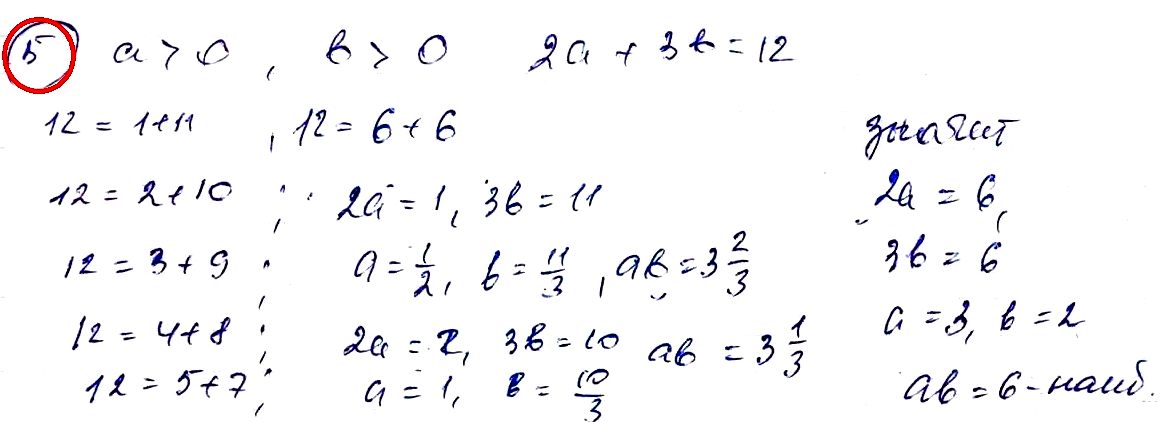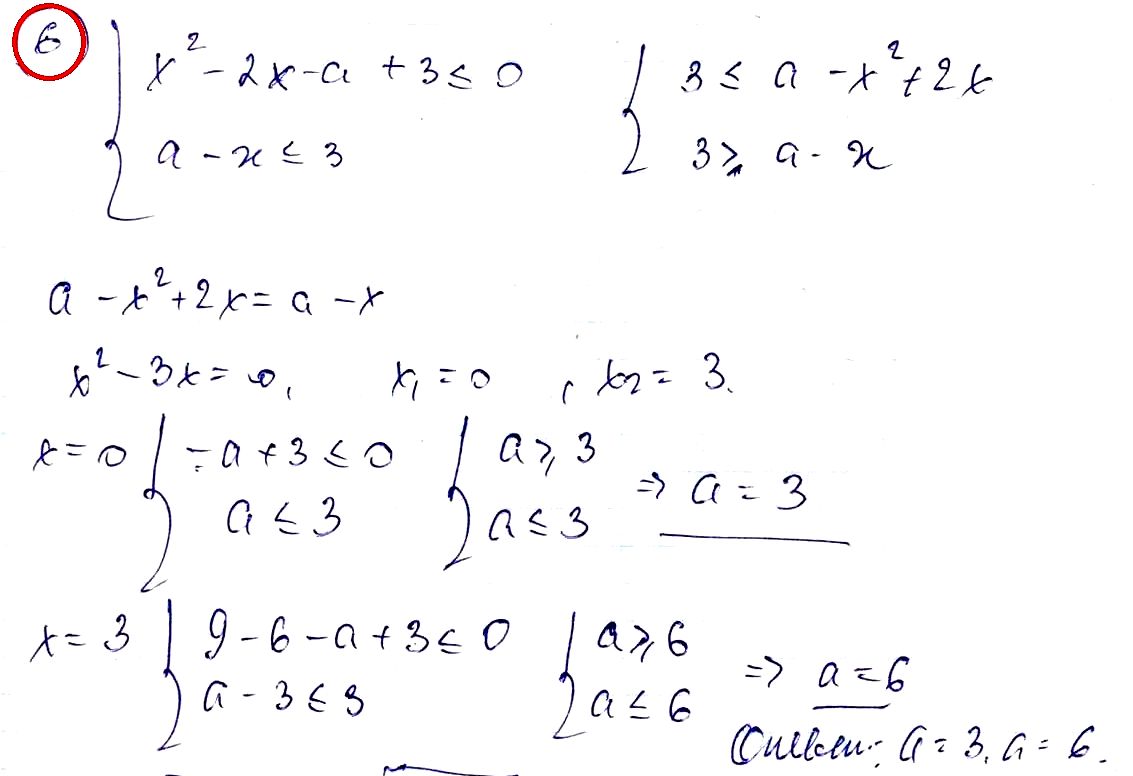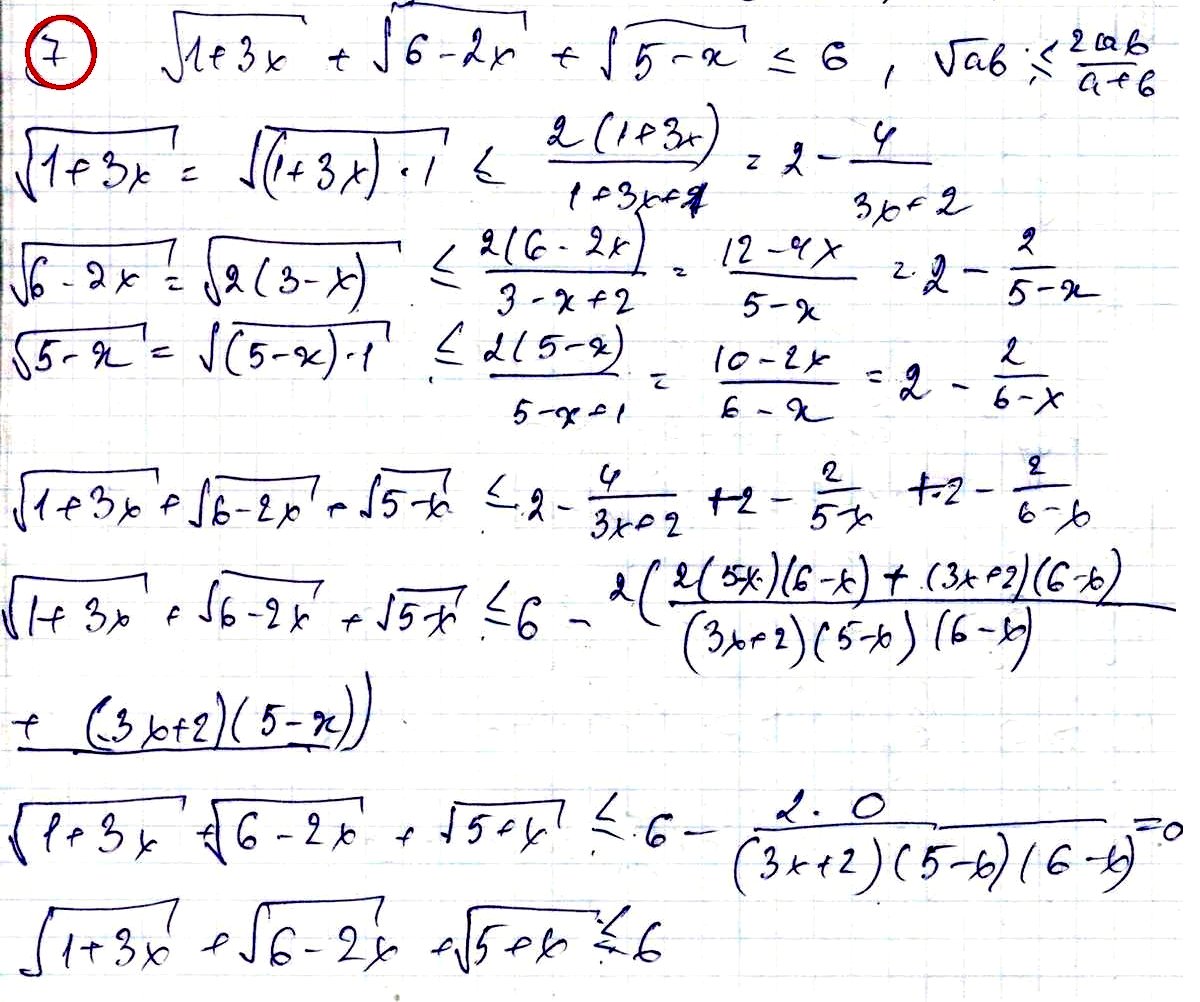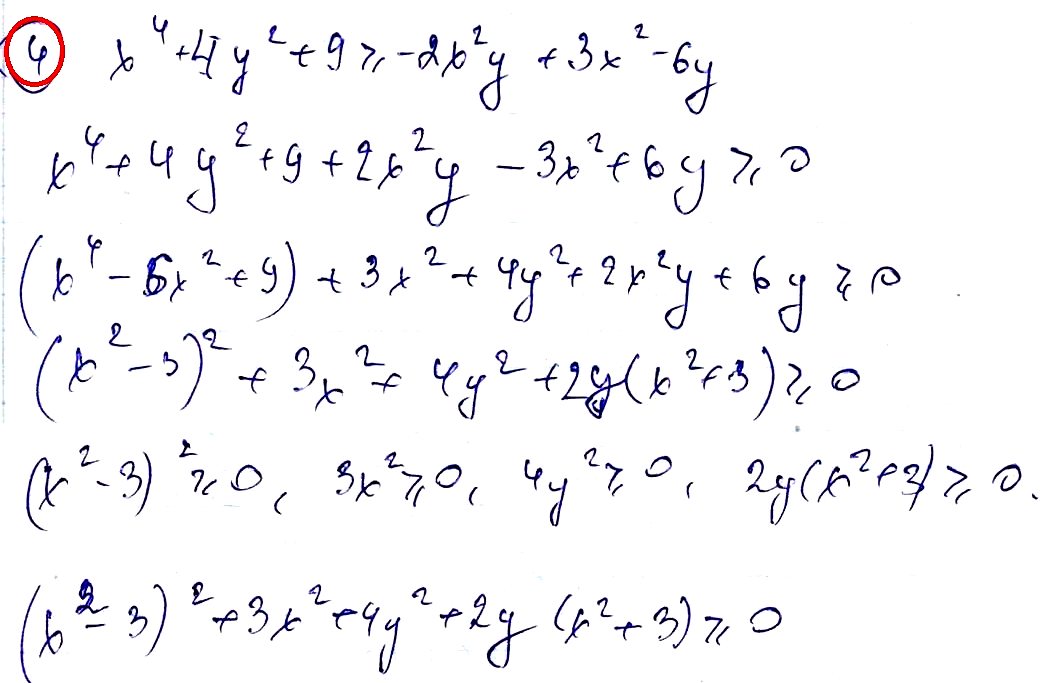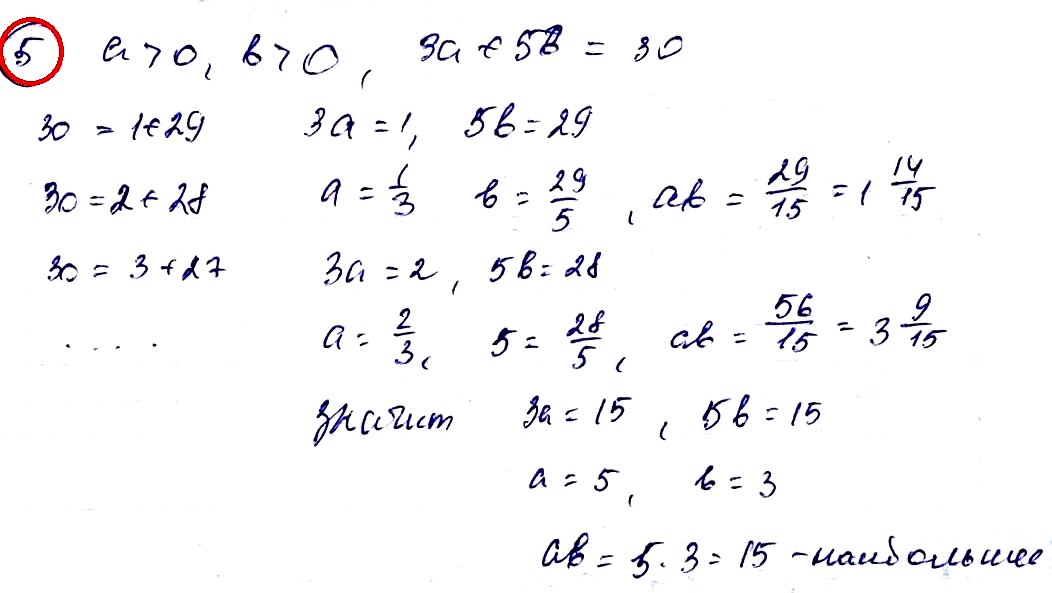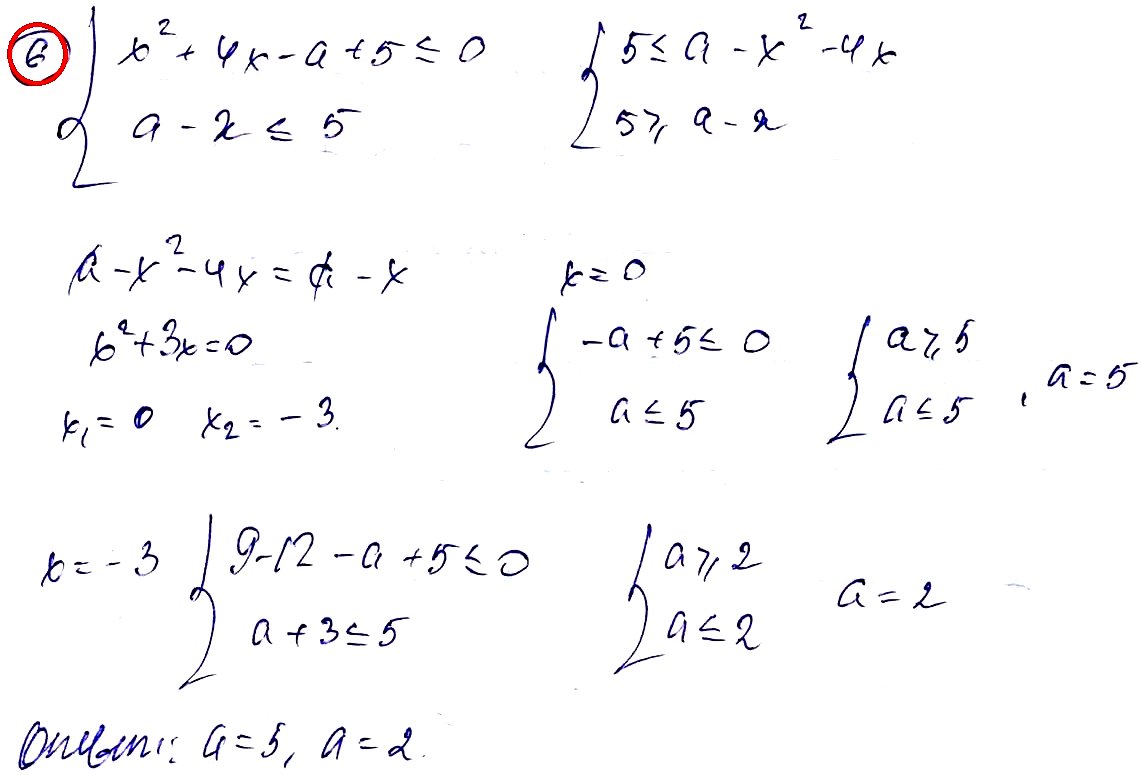Ответы на КР-4 Алгебра 9 (угл)

Алгебра 9 класс. Контрольная работа КР-4 «Неравенства с двумя переменными и их системы. Доказательства неравенств» для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и Ответы на КР-4 Алгебра.

 

Контрольная № 4
по алгебре в 9 классе (угл.)

Тема: Неравенства с двумя переменными и их системы. Доказательства неравенств

КР-4. Вариант 1

ОТВЕТЫ на Вариант 1

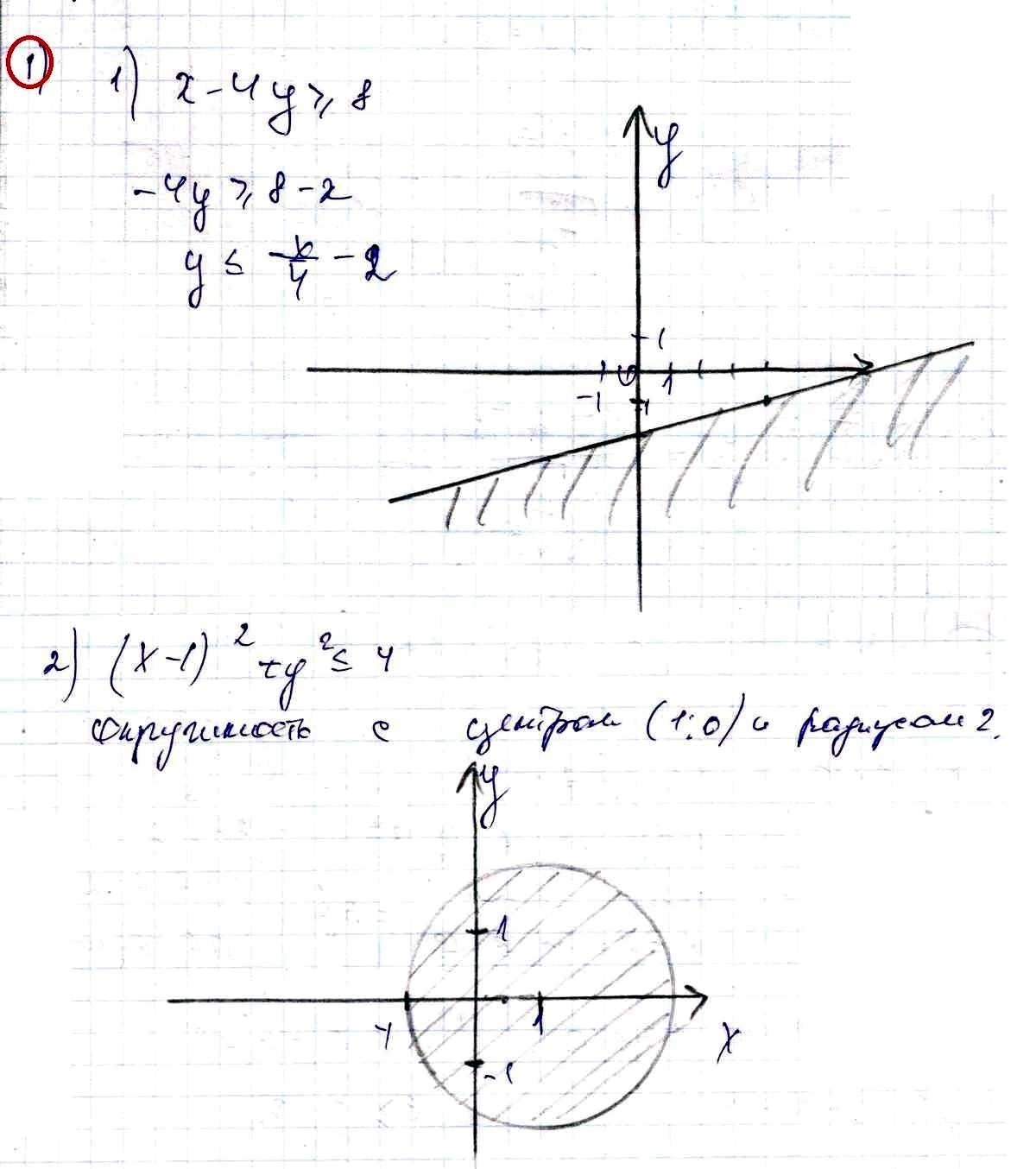
№ 1. Изобразите график неравенства:
1) х – 4у ≥ 8; 2) (х – 1)^2 + у^2 ≤ 4.

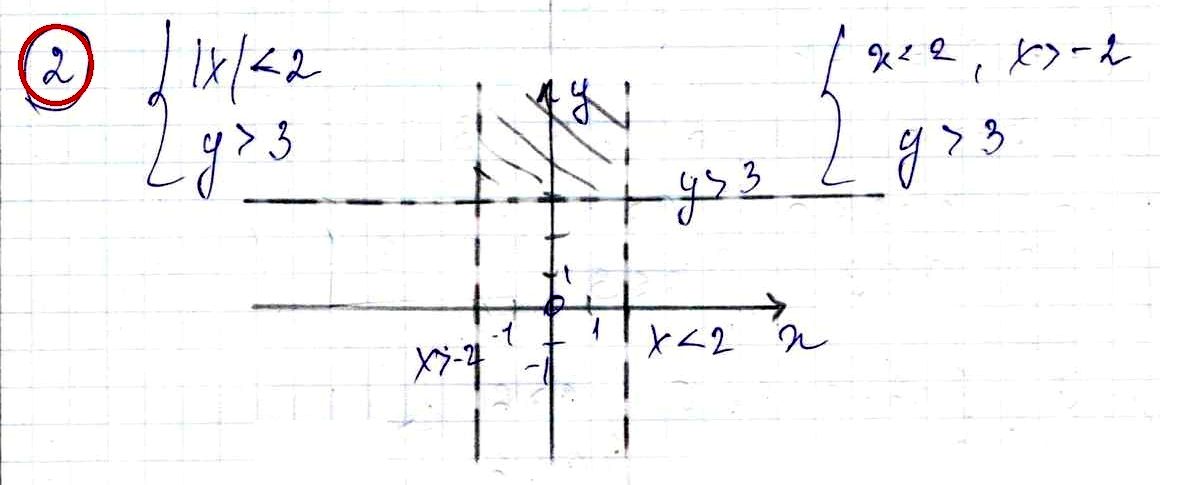
№ 2. Изобразите на координатной плоскости ху множество решений системы неравенств
{ |x| < 2,
{ y > 3.

№ 3. Задайте системой неравенств фигуру, изображённую на рисунке 9.
ОТВЕТ:
{ y ≤ 4,
{ y ≥ x².

№ 4. Докажите неравенство x^2 + 9y^4 + 1 ≥ –3ху^2 – х + 3у^2.

№ 5. Известно, что а > 0, b > 0 и 2а + 3b = 12. Найдите наибольшее значение выражения аb.
ОТВЕТ: 6.

№ 6. При каких значениях параметра а система неравенств имеет решение?
{ x^2 – 2x – a + 3 ≤ 0,
{ a – x ≤ 3.
ОТВЕТ: a = 3, a = 6.

№ 7. Докажите неравенство √[1 + 3x] + √[6 – 2x] + √[5 – x] ≤ 6.

---

 

КР-4. Вариант 2

ОТВЕТЫ на Вариант 2

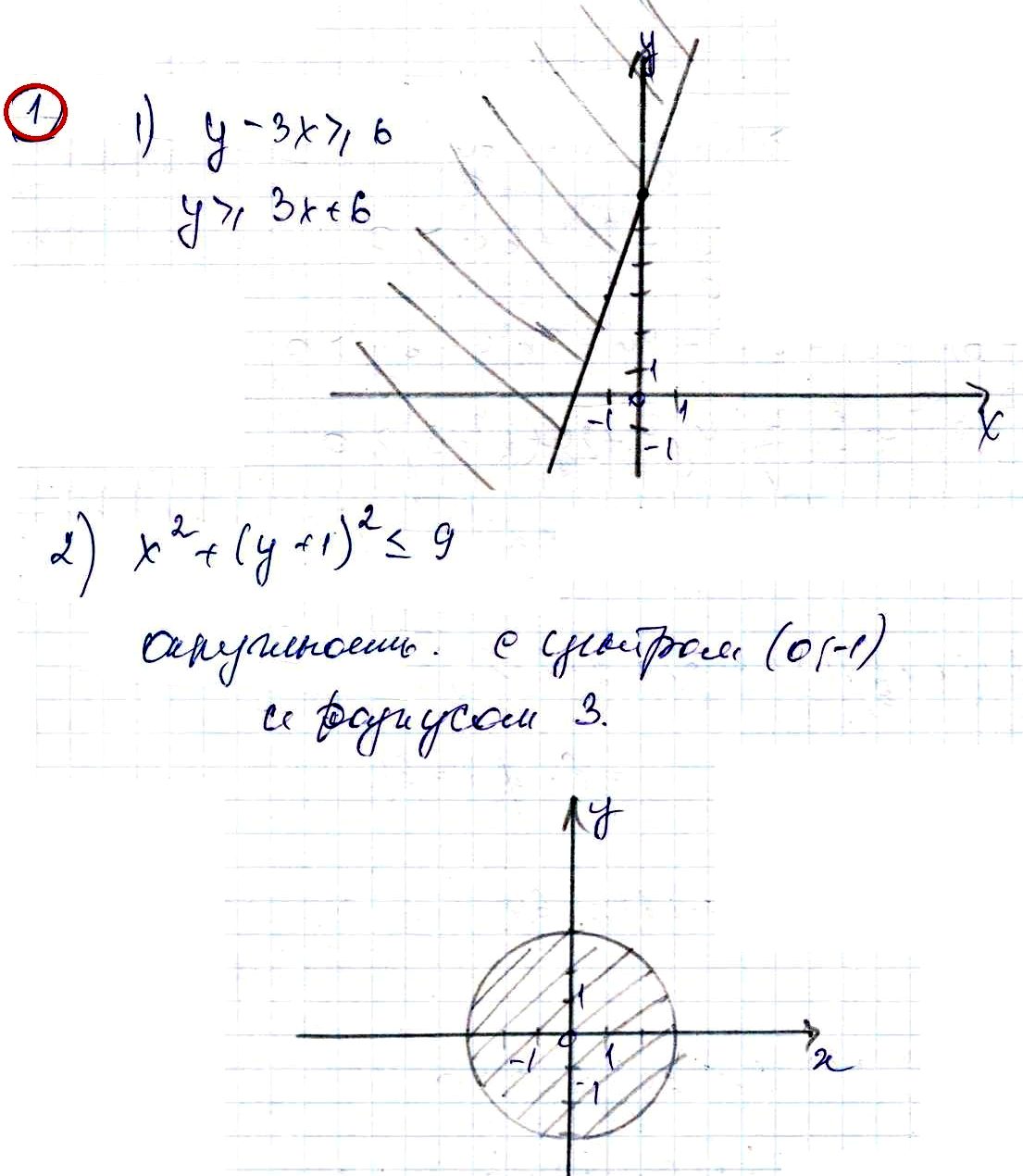
№ 1. Изобразите график неравенства:
1) у – 3х ≥ 6; 2) x² + (у + 1)² ≤ 9.

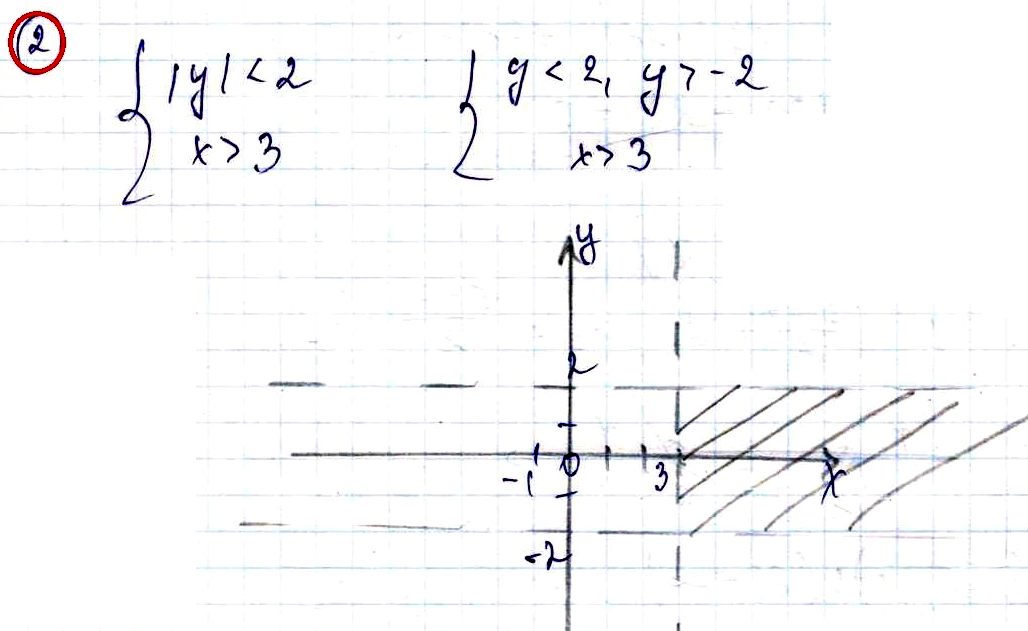
№ 2. Изобразите на координатной плоскости ху множество решений системы неравенств
{ |у| < 2,
{ х > 3.

№ 3. Задайте системой неравенств фигуру, изображённую на рисунке 10.
ОТВЕТ:
{ y ≤ 1,
{ y ≤ –x² + 1.

№ 4. Докажите неравенство х⁴ + 4у² + 9 ≥ –2x²у + 3x² – 6у.

№ 5. Известно, что а > 0, b > 0 и 3а + 5b = 30. Найдите наибольшее значение выражения аb.
ОТВЕТ: 15.

№ 6. При каких значениях параметра а система неравенств имеет решение?
{ x² + 4х – а + 5 ≤ 0,
{ а – х ≤ 5.
ОТВЕТ: a = 5, a = 2.

№ 7. Докажите неравенство √[1 – 3x] + √[6 + 2х] + √[5 + х] ≤ 6.

 

---

ГДЗ Контрольная работа № 4 «Неравенства с двумя переменными и их системы. Доказательства неравенств» для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + Решения и Ответы на КР-4 Алгебра 9 класс. Цитаты из пособия «Алгебра 9 класс Самостоятельные и контрольные работы»  (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях.

Вернуться к Списку контрольных работ для УМК Мерзляк, Поляков (угл.)