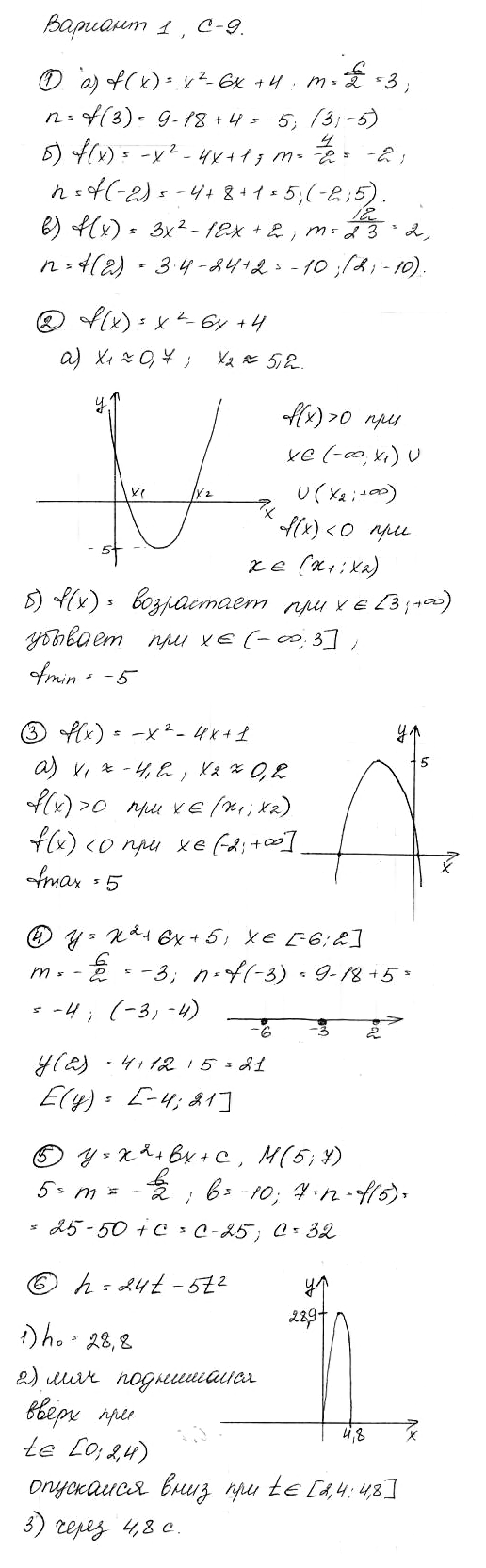Самостоятельная работа № 9 по алгебре в 9 классе «Построение графика квадратичной функции» с ответами (Варианты 1, 2). Дидактические материалы для учителей, учащихся и родителей. Упражнения в работе даны с избытком, поэтому каждый учитель самостоятельно определяет количество необходимых заданий в работе. Алгебра 9 Макарычев С-09.
Вернуться к Списку работ (в ОГЛАВЛЕНИЕ)
АЛГЕБРА 9 класс (Макарычев)
Самостоятельная работа № 9.
СР-9. Вариант 1 (задания)
Вариант 1. Транскрипт заданий
№ 1. Найдите координаты вершины параболы:
a) f(x) = x2 – 6х + 4;
б) f(х) = –x2 – 4х + 1;
в) f(x) = 3x2 – 12х + 2.
При вычислении воспользуйтесь формулами m = –b/2a и n = f(–b/2a), где m и n — координаты вершины параболы f(х) = аx2 + bx + с.
№ 2. Используя результаты вычислений в задании 1а, постройте график функции f(х) = x2 – 6х + 4. Найдите по графику:
а) нули функции; промежутки, в которых f(х) < 0 и f(х) > 0;
б) промежутки убывания и возрастания функции; наименьшее ее значение.
№ 3. Используя результаты вычислений в задании 16, постройте график функции f(x) = –x2 – 4х + 1. Найдите по графику:
а) нули функции; промежутки, в которых f(x) < 0 и f(x) > 0;
б) промежутки возрастания и убывания функции; наибольшее ее значение.
№ 4. Найдите область значений функции у = x2 + 6x + 5, где х е [–6; 2].
№ 5. При каких значениях b и с точка М (5; 7) является вершиной параболы у = x2 + bx + с?
№ 6. Мяч брошен вертикально вверх с начальной скоростью 24 м/с. Зависимость расстояния h(м) от мяча до земли от времени полета t(с) выражается формулой h = 24t – 5t2. Постройте график этой зависимости. Найдите по графику:
1) какой наибольшей высоты достиг мяч;
2) в какой промежуток времени он поднимался вверх и в какой опускался вниз;
3) через сколько секунд после броска мяч упал на землю.
ОТВЕТЫ на Вариант 1
СР-9. Вариант 2 (задания)
№ 1. Найдите координаты вершины параболы:
a) g(x) = x2 + 4х + 2; б) g(x) = –x2 – 6х + 3; в) g(x) = 4x2 – 8x – 1.
При вычислении воспользуйтесь формулами m = –b/2a и n = g(–b/2a), где m и n – координаты вершины параболы g(x) = ax2 + bx + с.
№ 2. Используя результаты вычислений в задании 1а, постройте график функции g(x) = x2 + 4х + 2. Найдите по графику:
а) нули функции; промежутки, в которых g(x) < 0 и g(x) > 0;
б) промежутки убывания и возрастания функции; наименьшее ее значение.
№ 3. Используя результаты вычислений в задании 16, постройте график функции g(x) = –x2 – 6х + 3. Найдите по графику:
а) нули функции; промежутки, в которых g(x) > 0 и g(x) < 0;
б) промежутки возрастания и убывания функции; наибольшее ее значение.
№ 4. Найдите область значений функции у = –x2 + 4х + 3, где х е [0; 5].
№ 5. При каких значениях b и с точка К (7; 2) является вершиной параболы у = x2 + bх + с?
№ 6. Из лука выпущена стрела вертикально вверх с начальной скоростью 50 м/с. Зависимость расстояния s (м) от стрелы до земли от времени полета t (с) выражается формулой s = 50t – 5t2. Постройте график этой зависимости. Найдите по графику:
1) какой наибольшей высоты достигла стрела;
2) в какой промежуток времени она поднималась вверх и в какой опускалась вниз;
3) через сколько секунд после пуска стрела упала на землю.
ОТВЕТЫ на Вариант 2
Вы смотрели: Самостоятельная работа № 9 по алгебре в 9 классе «Построение графика квадратичной функции» с ответами. Дидактические материалы для учителей, учащихся и родителей. Алгебра 9 Макарычев С-09.
Вернуться к Списку работ (в ОГЛАВЛЕНИЕ)