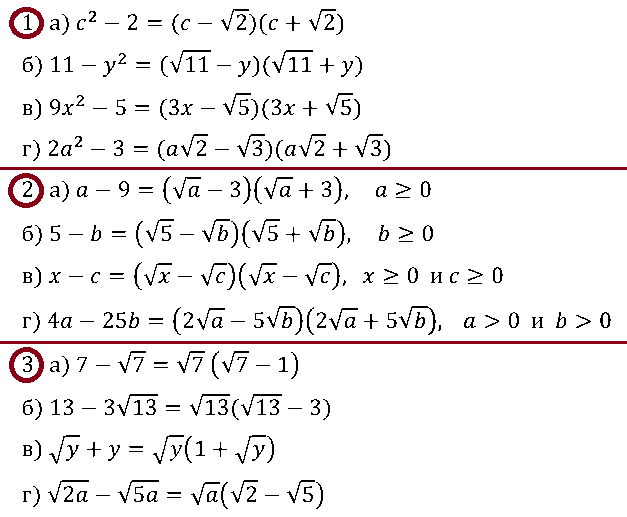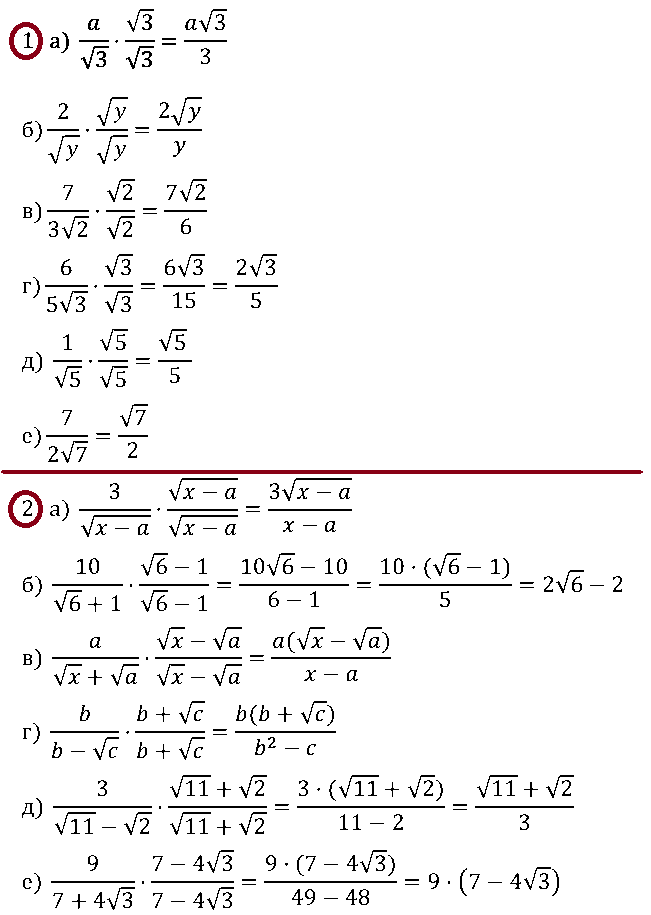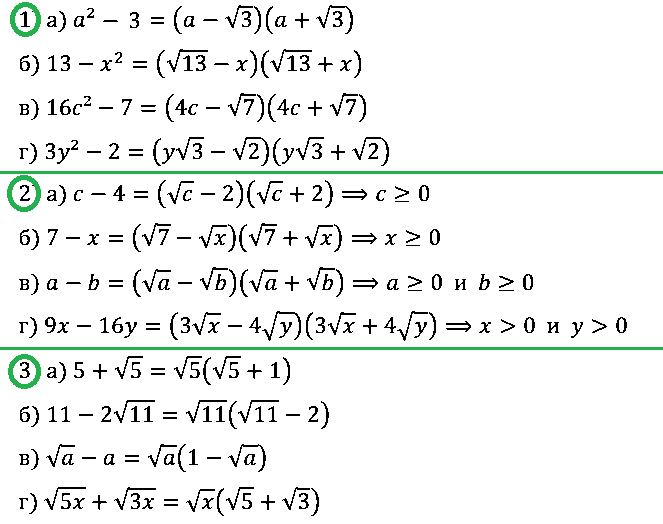Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ для УМК Макарычева по теме «Преобразование выражений, содержащих квадратные корни». Цитаты из пособия указаны в учебных целях. Алгебра 8 Макарычев Самостоятельная С-22 + решения.
Вернуться к Списку самостоятельных работ (в ОГЛАВЛЕНИЕ)
Самостоятельная работа № 22
Алгебра 8 класс (УМК Макарычев)
C-22. Вариант 1 (задания и ответы)
№ 1. Упростите выражение:
1) а) 3√c + 8√c – 9√c; б) 5√a – 2√b + √a; в) √4x + √64x – √81x; г) √27 – √48 + √75;
2) а) … ; 3) а) … .
№ 2. Выполните действия:
1) а) (2 + √3)(1 – √3); б) (√2 – √5)(2√2 + √5); в) (√7 – √12)( √7 – 3√3); г) (2√5 – √18)( √18 + √5) – √90;
2) … ; 3) … .
№ 3. Разложите на множители выражение:
1) а) с2 – 2; б) 11 – y2; в) 9x2 – 5; г) 2а2 – 3;
2) а) … ; 3) а) …
№ 4. Сократите дробь: а) (a2 – 3)/(a + √3); б) …
ОТВЕТ:
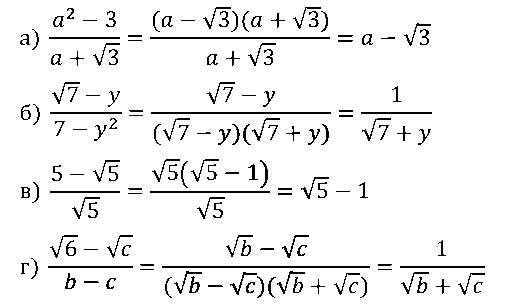
№ 5. Освободитесь от иррациональности в знаменателе дроби:
1) а) а/√3; б) 2/√y; в) 7/(3√2); г) 6/(5√3); д) 1/√5;
2) а) …
№ 6. Докажите, что верно равенство:
a) √[9 – 6√2] = √6 – √3; б) √[27 + 10√2] = √2 + 5.
ОТВЕТ:
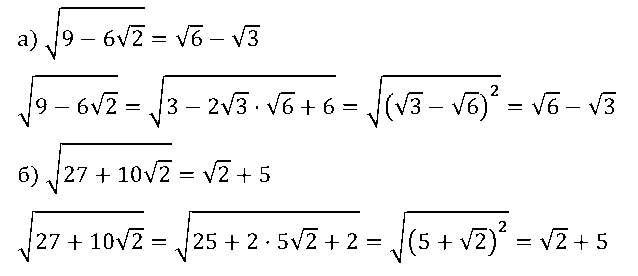
№ 7. Докажите, что значение выражения:
а) √[3 + 3√5] • √[3√5 – 3]; б) √[(√3 + 1) 2√2] • √[2√2 (√3 – 1)]
есть число натуральное.
ОТВЕТ:
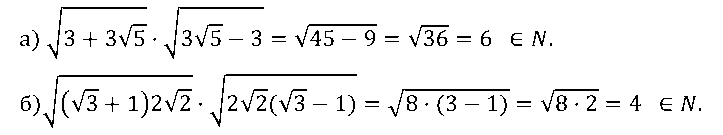
№ 8. Сократите дробь: а) (√15 – 5)/(3 – √15); …
ОТВЕТ:
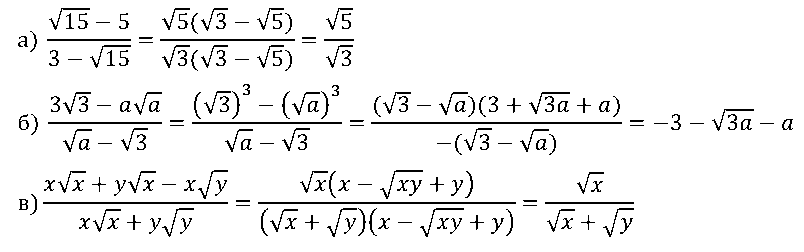
C-22. Вариант 2 (задания и ответы)
№ 1. Упростите выражение:
1) а) 2√а + 6√а – 7√а; б) 4√х + 2√х–5√х; в) √49с – √16с + √25с; г) √32+ √18 – √50;
2) … ; 3) … .
№ 2. Выполните действия:
1) a) (1 – √2) (3 + √2); б) (√3 + √7) (2√3 – √7); в) (√5 – √18) (√5 – 2√2); г) (2√7 + √12) (√12 – √7) – √84;
2) … ; 3) … .
№ 3. Разложите на множители выражение:
1) а) a2 – 3; б) 13 – x2; в) 16с2 – 7; г) 3y2 – 2;
2) … ; 3) … .
№ 4. Сократите дробь:
а) (с2 – 2)/(с – √2); б) (x + √5)/(x2 – 5); в) (7 + √7)/ √7; г) (а – у)/(√a + √y).
ОТВЕТ:
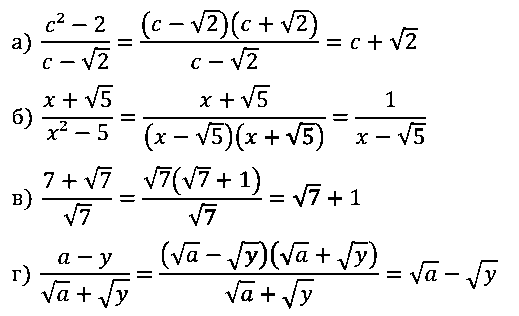
№ 5. Освободитесь от иррациональности в знаменателе дроби:
1) а) b/√7; б) 5/√x; в) 5/(3√6); г) 12/(7√2); д) 1/√3; е) 5/(4√5).
2) а) 2/√[c + y]; б) 6/(√5 + 1); в) c/(√a – √c); г) k/(x + √k); д) 5/(√13 + √3); е) 6/(5 – 2√6).
№ 6. Докажите, что верно равенство:
a) √[8 + 4√3] = √6 + √2; б) √[38 – 12√2] = 6 – √2.
ОТВЕТ:
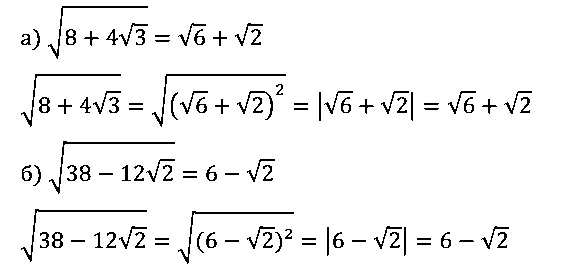
№ 7. Докажите, что значение выражения:
a) √[2•√5 – 2] • √[2 + 2√5]; б) √[(√5 – √2) • 3√З] • √[3√3 • (√2 + √5)]
есть число натуральное.
ОТВЕТ:
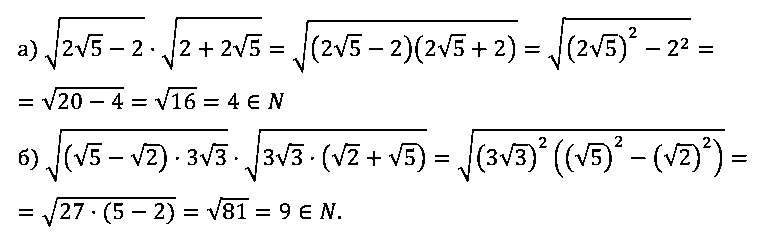
№ 8. Сократите дробь:
a) (√14 – 7) / (2 – √14); б) (√x + √2) / (2√2 + x√x);
в) (a√a – b√b) / (a√a + b√a + a√b).
ОТВЕТ:
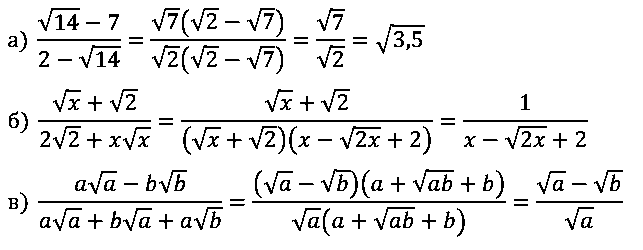
Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельная С-22 «Преобразование выражений, содержащих квадратные корни». Цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой. Цитаты из пособия указаны в учебных целях.
Вернуться к Списку самостоятельных работ (в ОГЛАВЛЕНИЕ)