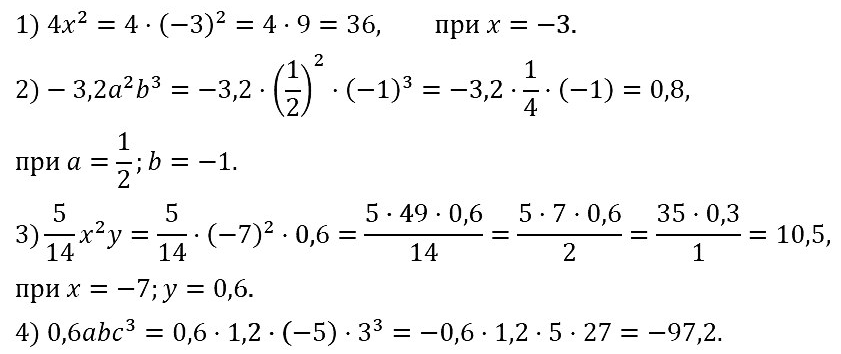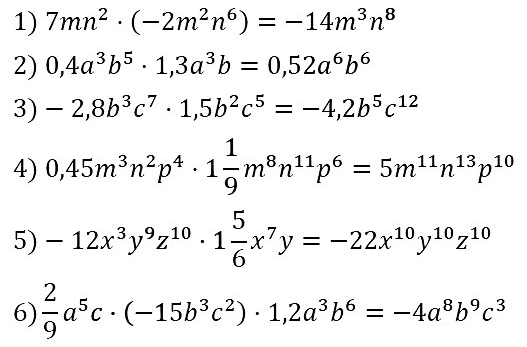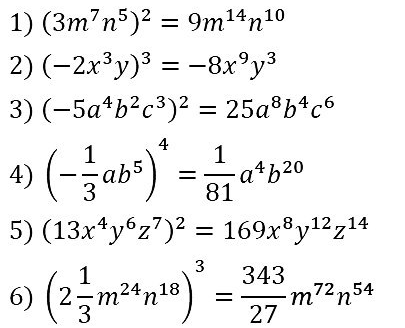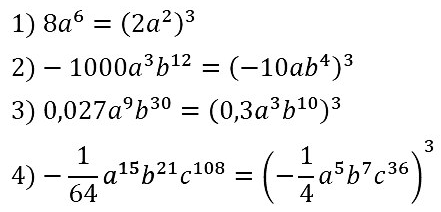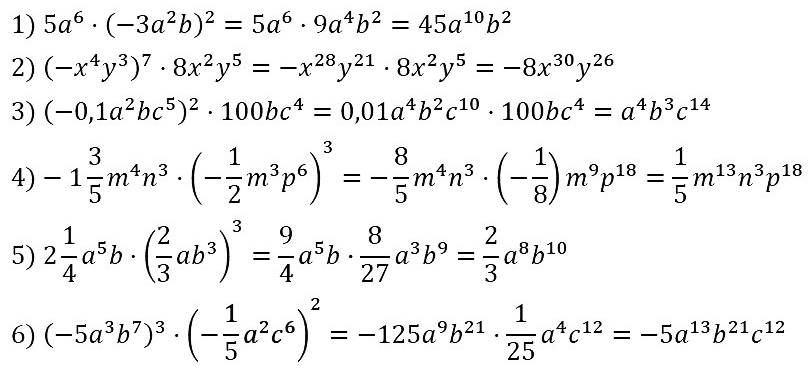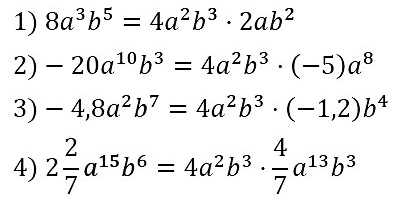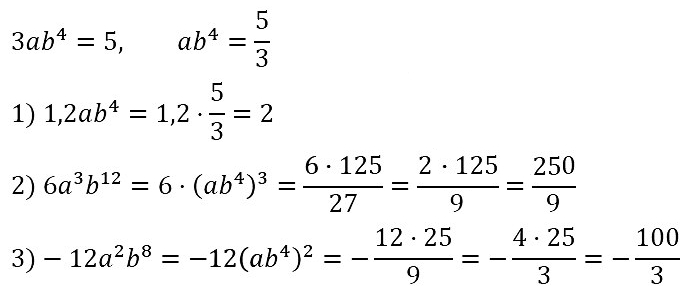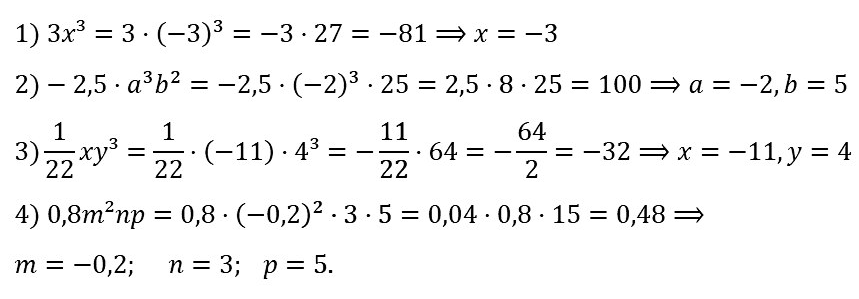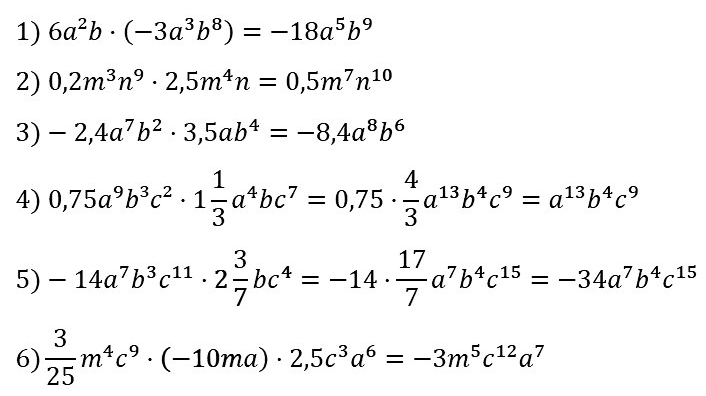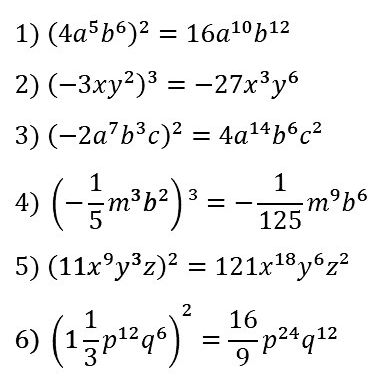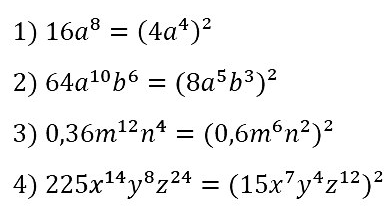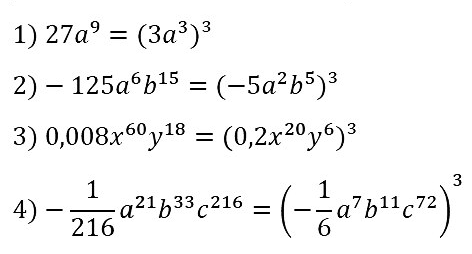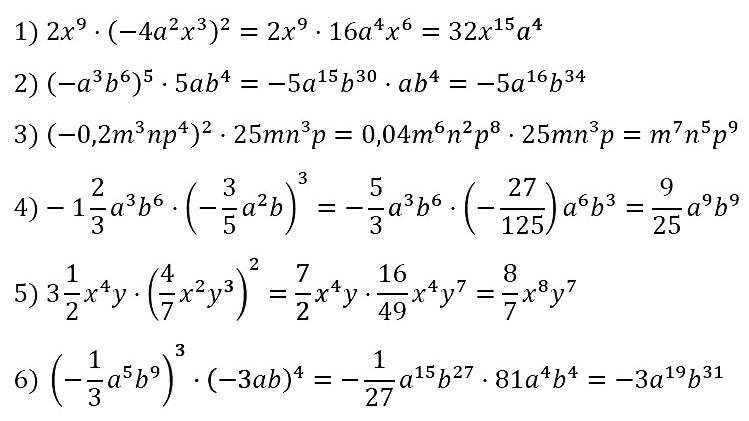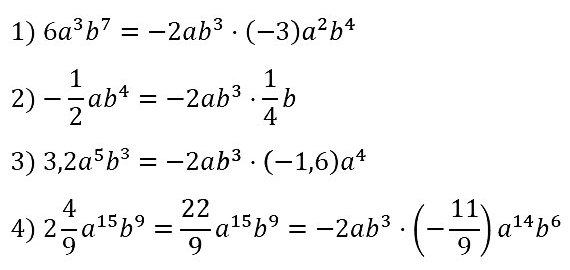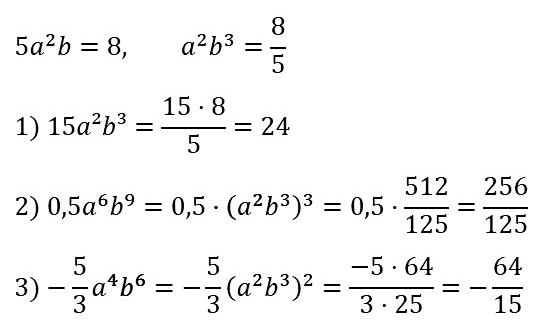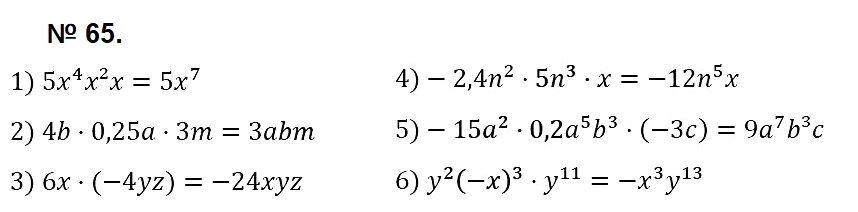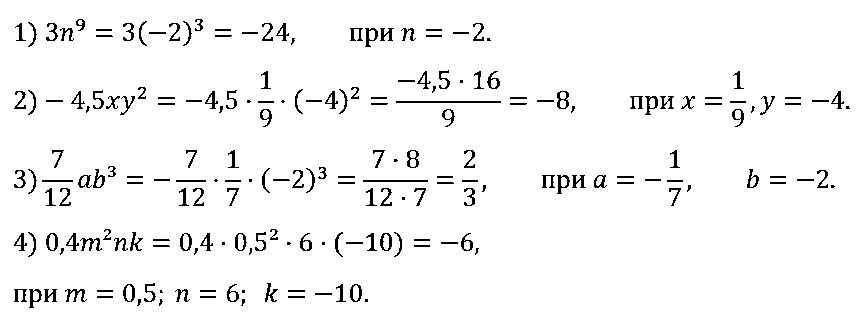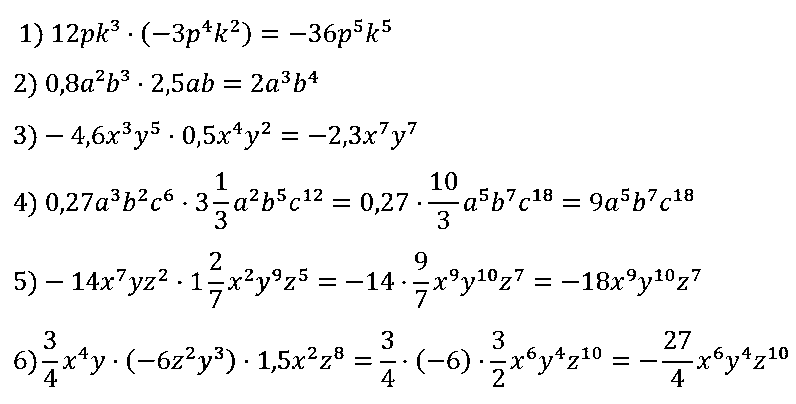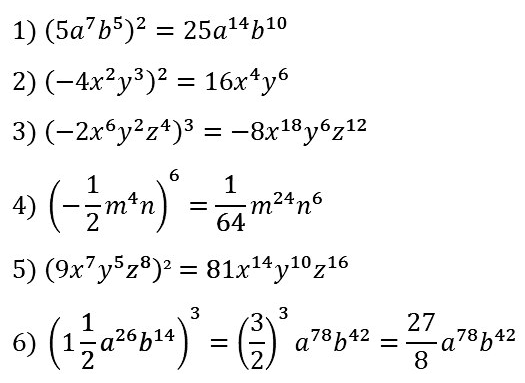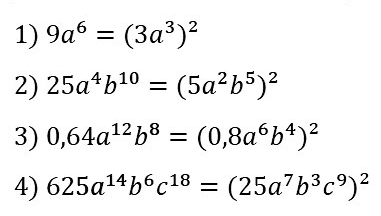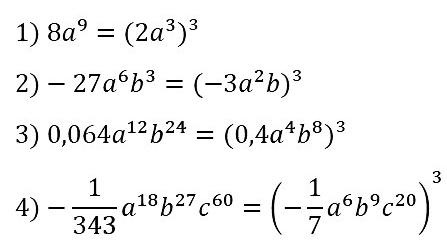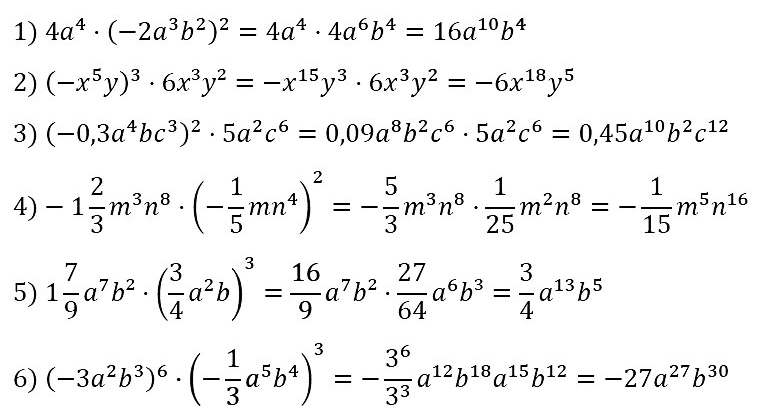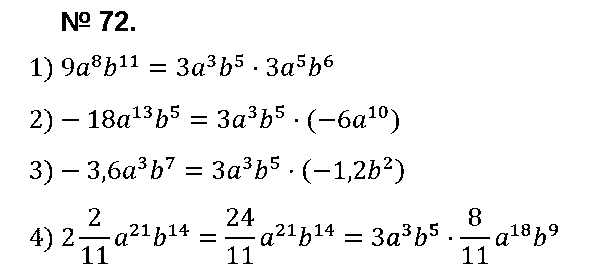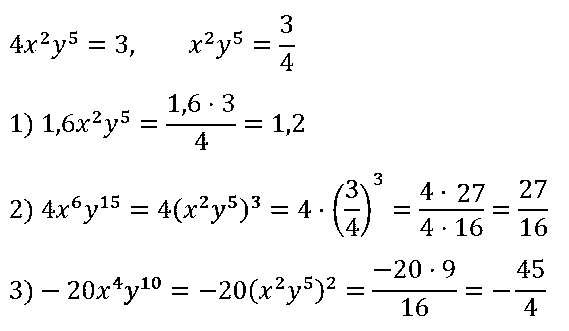Алгебра 7 Мерзляк С-09 «Одночлены» — цитаты из упражнений №№ 65-73 в 3-х вариантах для компиляции самостоятельных работ из пособия для учащихся «Алгебра 7 класс. Дидактические материалы / Мерзляк, Полонский, Рабинович, Якир». Цитаты из пособия указаны в учебных целях. Упражнения даны с избытком, поэтому учитель самостоятельно выбирает какие из указанных упражнений будут в вашей самостоятельной работе.
Вернуться к Списку самостоятельных работ
Самостоятельная № 9. Вариант 1
ОТВЕТЫ на Вариант 1
№ 65. Приведите одночлен к стандартному виду, укажите его коэффициент и степень:
1) 8х3хх5; 4) –2 1/3 • m2 • 6mn3;
2) 3а • 0,5b • 4с; 5) –2x3 • 0,1х3у • (–5у);
3) 3а • (–2ас); 6) р • (–q) • р20.
№ 66. Найдите значение одночлена:
1) 4x2, если х = –3;
2) –3,2a2b3, если а = 1/2, b = –1;
3) –5/14 • x2y, если х = –7, у = 0,6;
4) 0,6abc3, если а = 1,2, b = –5, с = 3.
№ 67. Выполните умножение одночленов:
1) 7mn2 • (–2m2n6); 4) 0,45m3n2р4 • 1 1/9 • m8n11р6;
2) 0,4a3b5 • 1,3a3b; 5) –12x3y9z10 • 1 5/6 • х7у;
3) –2,8b3с7 • 1,5b2с5; 6) 2/9 • а5с • (–15b3c2) • 1,2a3b6.
№ 68. Выполните возведение в степень:
1) (3m7m5)2; 3) (–5а4b2с3)2; 5) (13x5y6z7)2;
2) (–2х3у)3; 4) (–1/3 • ab5); 6) (2 1/3 • m24n18).
№ 69. Представьте в виде квадрата одночлена стандартного вида выражение:
1) 4а4; 2) 16а6b2; 3) 0,49а8b10; 4) 324а10b12с16.
ОТВЕТ: 1) 4а4 = (2a2)2;
2) 16а6b2 = (4a3b)2;
3) 0,49а8b10 = (0,7a4b5)2;
4) 324а10b12с16 = (18a5b6c8)2.
№ 70. Представьте в виде куба одночлена стандартного вида выражение:
1) 8а6; 2) –1000a3b12; 3) 0,027а9b30; 4) –1/64 • а15b21с108.
№ 71. Упростите выражение: 1) 5a6 • (–3а2b)2; 2) (–x4y3)7 • 8x2y5; …
№ 72. Представьте данное выражение в виде произведения двух одночленов, один из которых равен 4a2b3:
1) 8a3b5; 2) –20а10b3; 3) –4,8a2b7; 4) 2 2/7 • a15b6.
№ 73. Известно, что 3аb4 = 5. Найдите значение выражения:
1) 1,2аb4; 2) 6a3b12; 3) –12a2b8.
Самостоятельная № 9. Вариант 2
ОТВЕТЫ на Вариант 2
№ 65. Приведите одночлен к стандартному виду, укажите его коэффициент и степень:
1) 8y2у3у; 4) –2 2/3 • m4 • 9mn3;
2) 7х • 0,1y • 2z; 5) –3a2 • 0,2аb4 • (–10b);
3) 5b • (–3ab); 6) х3 • (–y)3 • х.
№ 66. Найдите значение одночлена:
1) 3х3, если х = –3;
2) –2,5a3b2, если а = –2, b = 5;
3) 1/22 • xy3, если х = –11, у = 4;
4) 0,8m2nр, если m = –0,2, n = 3, р = 5.
№ 67. Выполните умножение одночленов:
1) 6а2b • (–3a3b8); 4) 0,75a9b3c2 • 1 1/3 • а4bс7;
2) 0,2m3n9 • 2,5m4n; 5) –14а7b3с11 • 2 3/7 • bc4;
3) –2,4а7b2 • 3,5аb4; 6) 3/25 • m4с9 • (–10ma) • 2,5с3a6.
№ 68. Выполните возведение в степень: 1) (4a5b6)2; 2) (–3xy2)3; 3) (–2a7b3c)2; …
№ 69. Представьте в виде квадрата одночлена стандартного вида выражение:
1) 16a8; 2) 64a10b6; 3) 0,36m12n4; 4) 225x14y8z24.
№ 70. Представьте в виде куба одночлена стандартного вида выражение:
1) 27а9; 2) –125a6b15; 3) 0,008x60y18; 4) –1/216 • a21b33c216.
№ 71. Упростите выражение: 1) 2x9 • (–4a2x3)2; 2) (–a3b6)5 • 5ab4; …
№ 72. Представьте данное выражение в виде произведения двух одночленов, один из которых равен –2ab3:
1) 6a3b7; 2) –1/2 • ab4; 3) 3,2а5b3; 4) 2 4/9 • а15b9.
№ 73. Известно, что 5a2b3 = 8. Найдите значение выражения:
1) 15a2b3, 2) 0,5а6b9; 3) –5/3 • а4b6.
Самостоятельная № 9. Вариант 3
ОТВЕТЫ на Вариант 3
№ 65. Приведите одночлен к стандартному виду, укажите его коэффициент и степень:
1) 5х4x2х; 4) –2,4n2 • 5n3 • х;
2) 4b • 0,25а • 3m; 5) –15a2 • 0,2а5b3 • (–3c);
3) 6х • (–4yz); 6) y2(–х3) • у11.
№ 66. Найдите значение одночлена:
1) 3n3, если n = –2;
2) –4,5хy2, если х = 1/9, у = –4;
3) 7/12 • ab3, если а = –1/7, b = –2;
4) 0,4m2nk, если m = 0,5, n = 6, k = –10.
№ 67. Выполните умножение одночленов:
1) 12pk3 • (–3p4k2); 2) 0,8a2b3 • 2,5аb;
3) –4,6х3у5 • 0,5х4y2; 4) 0,27a3b2с6 • 3 1/3 • a2b5с12;
5) –14x7yz2 • 1 2/7 • x2y9z5; 6) 3/4 • х4у • (–6z2y3) • 1,5x2z8.
№ 68. Выполните возведение в степень: 1) (5a7b5)2; 2) (–4x2y3)2; …
№ 69. Представьте в виде квадрата одночлена стандартного вида выражение: 1) 9а6; 2) 25а4b10; 3) 0,64а12b8; 4) 625а14b6с18.
№ 70. Представьте в виде куба одночлена стандартного вида выражение:
1) 8а9; 2) –27а6b3; 3) 0,064а12b24; 4) –1/343 • a18b27с60.
№ 71. Упростите выражение: 1) 4a4 • (–2a3b2)2; 2) (–x5y)3 • 6x3y2; …
№ 72. Представьте данное выражение в виде произведения двух одночленов, один из которых равен 3a3b5:
1) 9а8b11; 2) –18а13b5; 3) –3,6a3b7; 4) 2 2/11 • a21b14.
№ 73. Известно, что 4x2у5 = 3. Найдите значение выражения:
1) 1,6x2у5; 2) 4х6у15; 3) –20х4у10.
Вы смотрели страницу СР-09 «Одночлены«. Цитаты упражнений из пособия для учащихся «Алгебра 7 класс. Дидактические материалы / Мерзляк и др.», которое используется в комплекте с учебником «Алгебра 7 класс Мерзляк».
Вернуться к Списку самостоятельных работ (Алгебра 7 класс Мерзляк)