Алгебра. Мерзляк 9 класс Контрольная 1 в 4-х вариантах (вариант 1). Контрольная работа по алгебре в 9 классе «Неравенства» для УМК Мерзляк, Полонский, Якир. Транскрипт заданий + Ответы.
Другие варианты:
КР-1. Вариант 2 КР-1. Вариант 3 КР-1. Вариант 4
Вернуться к Списку контрольных работ
Алгебра 9 класс (УМК Мерзляк)
Контрольная № 1. Вариант 1
Неравенства

Ответы на КР-1 Вариант 1
№ 1. Докажите неравенство (a – 4)2 > a(a – 8).
ОТВЕТ: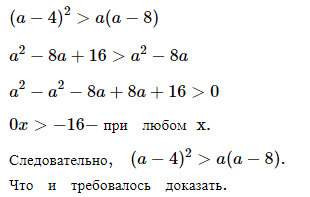
№ 2. Известно, что 3 < m < 6 и 4 < n < 5. Оцените значение выражения: 1) 3m + n; 2) mn; 3) m – n.
ОТВЕТ: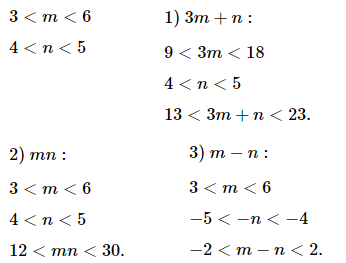
№ 3. Решите неравенство: 1) –2x > 8; 2) 6 + x > 3 – 2x.
ОТВЕТ: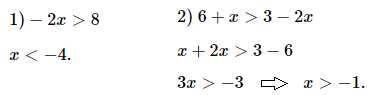
№ 4. Решите систему неравенств:
1) { 5x – 20 < 0, { 3x + 18 > 0;
2) { 2x + 40 > 30, { 21 – 4x < 5.
ОТВЕТ: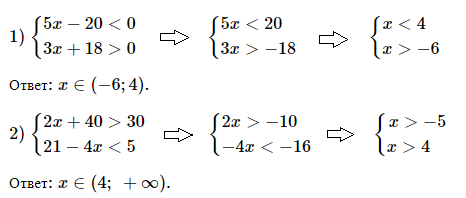
№ 5. Найдите множество решений неравенства:
1) 2x/3 – (x – 1)/6 + (x + 2)/2 ≥ 0;
2) 4x + 3 > 2(3x – 4) – 2x.
ОТВЕТ: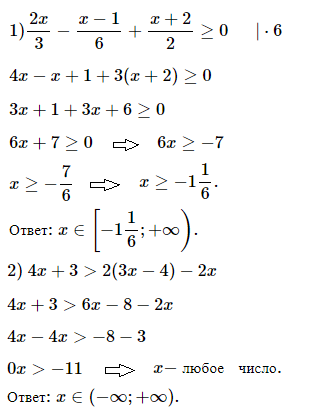
№ 6. Найдите целые решения системы неравенств
{ 5x –1 > 2x + 4,
{ x(x – 6) – (x + 2) (x – 3) > x – 30.
ОТВЕТ: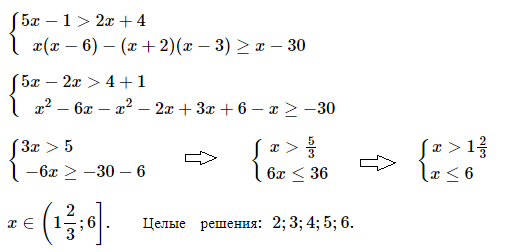
№ 7. При каких значениях переменной имеет смысл выражение
√[2 x + 5] + 4/√[7 – x] ?
ОТВЕТ: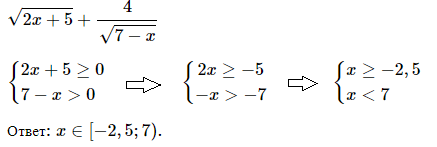
№ 8. Докажите неравенство 26a2 + 10ab + b2 + 2a + 4 > 0.
ОТВЕТ:
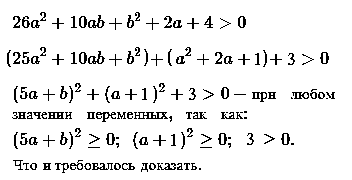
Смотрите также:
КР-1. Вариант 2 КР-1. Вариант 3 КР-1. Вариант 4
Вернуться к Списку контрольных работ
Вы смотрели: Контрольную работу по алгебре «Неравенства» с ответами Вариант 1. Мерзляк 9 класс Контрольная 1 из Методического пособия Буцко в 4-х вариантах. Контрольная работа по алгебре в 9 классе «Неравенства» для УМК Мерзляк, Полонский, Якир. Транскрипт заданий. Цитаты из пособия «Алгебра 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
Добавьте ответы по всем вариантом.
Добавили.
в 1 варианте в 8 задании неверный ответ. мы должны разложить a2 + 2a + 4 на a2 +2a + 1 + 3, тогда квадрат суммы не получится)
Исправлено.
добавьте рисунки после систем
Спс вам, за ответы и особенно за решения. Продолжайте в том же духе. И желательно сделать решение по геометрии, а то там только ответы:)
спасибо за ответы Коробейников Иван