Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельная С-26 «Решение квадратных уравнений (продолжение)». Цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой. Цитаты из пособия указаны в учебных целях. При постоянном использовании данных самостоятельных работ по алгебре в 8 классе необходимо купить книгу.
Самостоятельная работа № 26
(8 класс, УМК Макарычев и др.)
С-26 Вариант 1 (задания)
С-26 Вариант 2 (задания)
Ответы на самостоятельную работу
ОТВЕТЫ на Вариант 1
№ 1. Найдите корни уравнения:
1) а) (х – 2)2 = 3х – 8; б) (х – 1)2 = 29 – 5х; в) 5(х + 2)2 = – 6х – 44; г) (х + З)2 – 16 = (1 – 2х)2;
2) а) (х – 2)(х + 2) = 7х – 14; б) (–х – 1)(х – 4) = х(4х – 11); в) –х(1/3 – х) = (х – 1)(х + 1); г) 5(х – 2) = (3х + 2)(х – 2);
3) а) (x2 – x)/3 = (2х – 4)/5; б) (х2 – 3)/2 – 6х = 5; в) (x2 + 2х)/2 = (x2 + 24)/7; г) (3x2 + х)/4 – (2 – 7х)/5 = (3x2 + 17)/10.
№ 2. При каких значениях у:
а) значение многочлена у2 – 11у + 2,4 равно нулю;
б) равны значения двучленов 1,5у2 + 0,5 и 3у – 2,5у2;
в) трехчлен 2 + у – 0,5у2 равен двучлену 2у2 – Зу?
№ 3. Найдите корни уравнения и укажите их приближенные значения в виде десятичных дробей с точностью до 0,001:
а) x2 – 6х + 4 = 0; б) 16у2 – 8у – 31 = 0.
№ 4. Докажите, что при любом значении k уравнение 3y2 – ky – 2 = 0 имеет два корня.
№ 5. Докажите, что не существует такого значения m, при котором уравнение x2 – mх + m – 2 = 0 имело бы один корень.
№ 6. Решите уравнение: а) x3/|x| + х + 3 = 0; б) 3x2 + x2/|x| – 4 = 0.
ОТВЕТЫ на Вариант 2
№ 1. Найдите корни уравнения:
1) а) (х + 3)2 = 2х + 6; б) (х + 2)2 = 43 – 6х; в) 4(х – 1)2 = 12х + 3; г) (x – 2)2 + 24 = (2 + 3х)2;
2) a) (x – 3)(x + 3) = 5x – 13; б) 7(1 – x) = (2x + 3)(1 – x); в) –х(4х + 1) = (х + 2)(х – 2); г) (х + 4)(2х – 1) = х(3х +11);
3) a) (2x2 + х)/5 = (4х – 2)/3; б) (x2 – 4)/3 + 4х = 3; в) (x2 – 11)/7 = (х – x2)/2; г) (4x2 + х)/3 – (5х – 1)/6 = (x2 + 17)/9.
№ 2. При каких значениях а:
а) значение многочлена а2 – 11а + 2,8 равно нулю;
б) равны значения двучленов а2 – 6а и 0,5а2 – 16;
в) двучлен 2а2 – 1,6а равен трехчлену 1,8а2 + 0,4а + 5?
№ 3. Найдите корни уравнения и укажите их приближенные значения в виде десятичных дробей с точностью до 0,001: а) x2 – 4х – 3 = 0; б) 9y2 + 6у – 17 = 0.
№ 4. Докажите, что при любом значении m уравнение 4y2 + mу –5 = 0 имеет два корня.
№ 5. Докажите, что не существует такого значения а, при котором уравнение x2(а – 2) + ах + 1 = 0 имело бы один корень.
№ 6. Решите уравнение: а) x3/|x| + 3х + 2 = 0; б) x2 + x2/|x| – 6 = 0.
Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельная С-26 «Решение квадратных уравнений (продолжение)». Цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой. Цитаты из пособия указаны в учебных целях.
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Макарычев и др.)



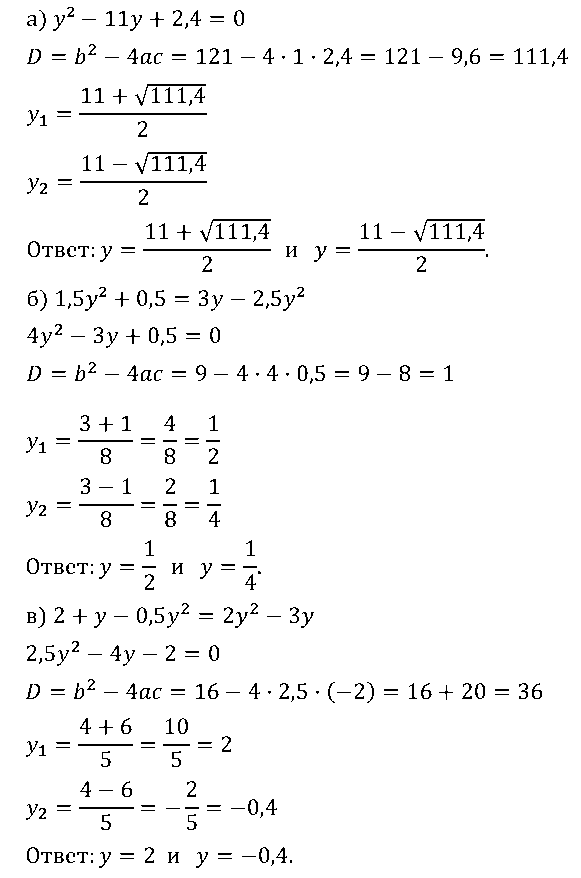
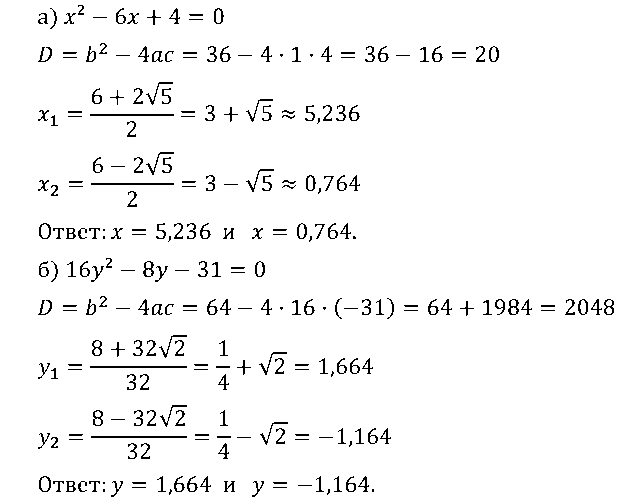
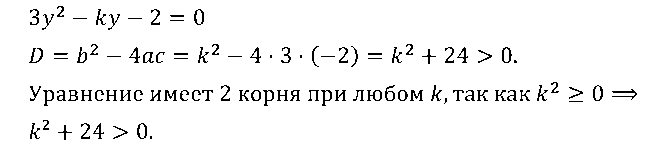
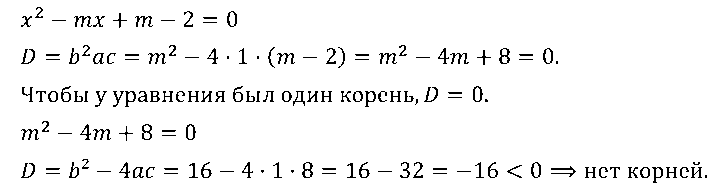

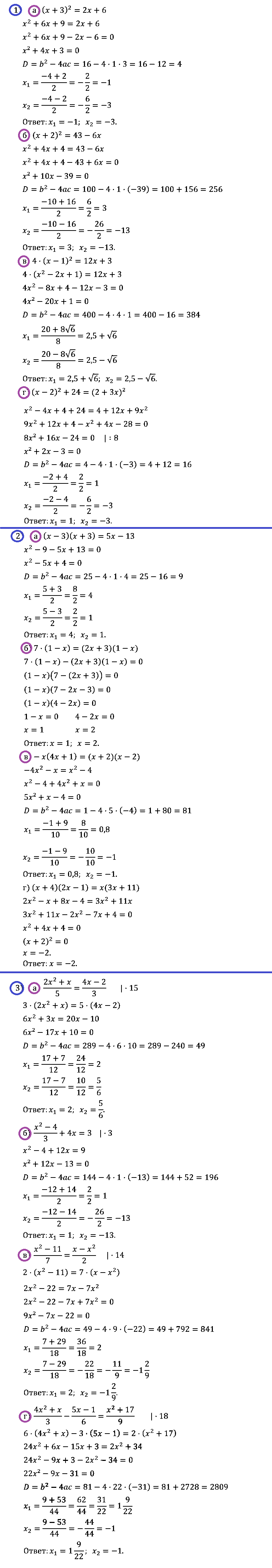
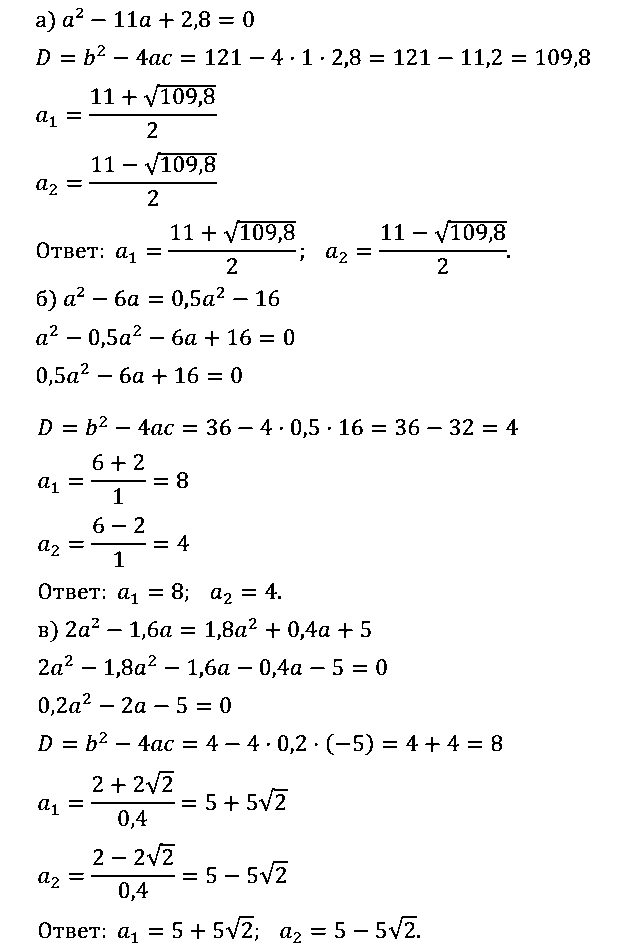
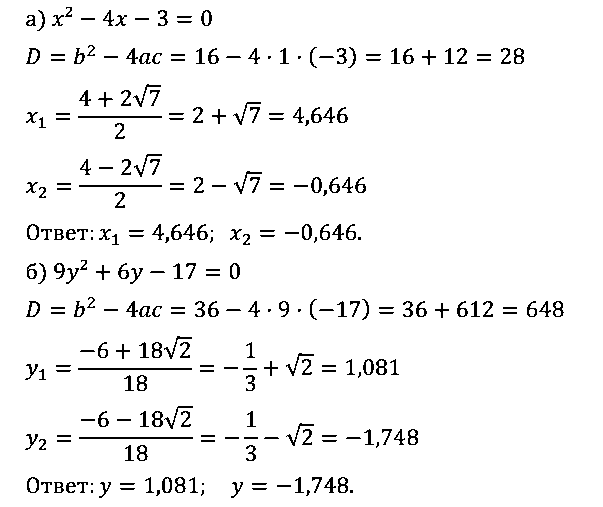
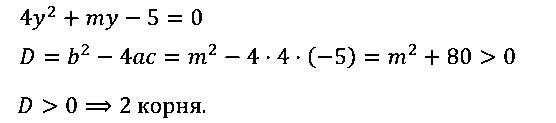
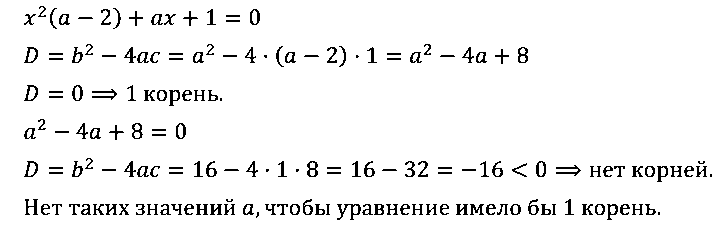

Спасибо