Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельная С-23 «Уравнения и их корни». Цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой. Цитаты из пособия указаны в учебных целях. При постоянном использовании данных самостоятельных работ по алгебре в 8 классе необходимо купить книгу.
Самостоятельная работа по алгебре
(8 класс, УМК Макарычев и др.)
С-23 Вариант 1 (задания)
№ 1. Является ли число а корнем уравнения:
а) 2х – 7 = 8, а = 7,5;
б) x3 – 2,5 = –29,5, а = –3;
в) x2 –х – 20 = 0, а = 5;
г) х4 – x3 + 2х = 12, а = 2;
д) (x3 + 12)(x2 – 8) = 0, а = 2√2?
№ 2. Найдите корни уравнения:
а) (х – 3)(х + 12) = 0;
б) (х + 1)(х + 7)(х – 9) = 0;
в) (6х – 5)(х + 5) = 0;
г) (х + 8)(2х – 5)(x2 + 25) = 0.
№ 3. Докажите, что уравнение не имеет корней:
а) x2 + 10 = 0; б) √x + 4 = 0;
в) (5x – 1)/(x – 0,2) = 0; г) (10x + 7)/((x + 6)(x + 0,7)) = 0.
№ 4. Равносильны ли уравнения:
а) 5х – 7 = 0 и 1,4 – х = 0;
б) (6х – 18)(√x – 11) = 0 и (121 – x)(√x – 3) = 0;
в) x2 + 7 = 0 и √x + 49 = 0?
С-23 Вариант 2 (задания)
№ 1. Является ли число m корнем уравнения:
а) 9 – 4х = –5, m = 3,5;
б) х4 – 9,5 = 6,5, m = – 2;
в) х – x3 + 120 = 0, m = 5;
г) х4 – 3x2 + 5х = – 7, m = –1;
д) (x3 – 4)(x2 – 27) = 0, m = 3√3?
№ 2. Найдите корни уравнения:
а) (х + 2)(х – 7) = 0; б) (х – 1)(х + 5)(х – 8) = 0;
в) (3х – 1)(х + 4) = 0; г) (2х – 3)(x2 + 9)(х + 5) = 0.
№ 3. Докажите, что уравнение не имеет корней:
а) x2 + 1 = 0; б) √x + 9 = 0;
в) (2x + 1)/(x + 0,5) =0; г) (5x – 4)/((x + 2)(x – 0,8)) = 0.
№ 4. Равносильны ли уравнения:
а) 6x – 5 = 0 и 5/6 – х = 0;
б) (3х – 12)(√х – 13) = 0 и (х – 169)(√х – 2) = 0;
в) √x + 25 = 0 и x2 + 5 = 0?
ОТВЕТЫ НА САМОСТОЯТЕЛЬНУЮ РАБОТУ
ОТВЕТЫ на Вариант 1
№ 1. Является ли число а корнем уравнения: а) 2х – 7 = 8, а = 7,5; б) x3 – 2,5 = –29,5, а = –3; в) x2 –х – 20 = 0, а = 5; г) х4 – x3 + 2х = 12, а = 2; д) (x3 + 12)(x2 – 8) = 0, а = 2√2?
ОТВЕТЫ: а) да; б) да; в) да; г) да; д) да.
№ 2. Найдите корни уравнения: а) (х – 3)(х + 12) = 0; б) (х + 1)(х + 7)(х – 9) = 0; в) (6х – 5)(х + 5) = 0; г) (х + 8)(2х – 5)(x2 + 25) = 0.
РЕШЕНИЕ:
а) (х – 3) (х + 12) = 0; х = 3 и х = –12.
б) (х + 1) (х + 7) (х – 9) = 0; . х = –1, х = –7 и х = 9.
в) (6х – 5) (х + 5) = 0, х = 5/6 и х = –5.
г) (x + 8) (2x – 5) (х2 + 25) = 0; х = – 8 и х = 5/2 = 2 1/2.
№ 3. Докажите, что уравнение не имеет корней: а) x2 + 10 = 0; б) √x + 4 = 0; в) (5x – 1)/(x – 0,2) = 0; г) (10x + 7)/((x + 6)(x + 0,7)) = 0.
РЕШЕНИЕ:
а) х2 + 10 = 0; х2 = –10 не имеет корней, так как х2 > 0 для любого х.
б) √х + 4 = 0; √х = –4 не имеет корней, так как √х ≥ 0 для любого х.
в) (5x – 1)/(x – 0,2) = 5(x – 0,2)/(x – 0,2) = 5 ≠ 0.
г) (10x + 7)/((х + 6)(x + 0,7)) = 10(x + 0,7)/((х + 6)(x + 0,7)) = 10/(х + 6) ≠ 0
№ 4. Равносильны ли уравнения: а) 5х – 7 = 0 и 1,4 – х = 0; б) (6х – 18)(√x – 11) = 0 и (121 – x)(√x – 3) = 0; в) x2 + 7 = 0 и √x + 49 = 0?
РЕШЕНИЕ:
а) 5x – 7 = 5(x – 1,4) = 0 и 1,4 – х = 0 – равносильны.
б) (6x – 18) (√х – 11) = 0 и (121 – х) (√х – 3) = 0 – неравносильны.
в) х2 + 7 = 0 и √х + 49 = 0 – равносильны.
ОТВЕТЫ на Вариант 2
№ 1. Является ли число m корнем уравнения:
а) 9 – 4х = –5, m = 3,5; б) х4 – 9,5 = 6,5, m = – 2; в) х – x3 + 120 = 0, m = 5; г) х4 – 3x2 + 5х = – 7, m = –1; д) (x3 – 4)(x2 – 27) = 0, m = 3√3?
ОТВЕТЫ: а) да; б) да; в) да; г) да; д) да.
№ 2. Найдите корни уравнения:
а) (х + 2)(х – 7) = 0; б) (х – 1)(х + 5)(х – 8) = 0; в) (3х – 1)(х + 4) = 0; г) (2х – 3)(x2 + 9)(х + 5) = 0.
РЕШЕНИЕ:
а) (х + 2) (х – 7) = 0; х = –2 и х = 7.
б) (x – 1) (x + 5) (х – 8) = 0; х = 1, х = –5 и х = 8.
в) (3х – 1) (х + 4) = 0; х = –4 и х = 1/3.
г) (2х – 3) (х2 + 9) (х + 5) = 0; х = –5 и х = 1 1/2.
№ 3. Докажите, что уравнение не имеет корней:
а) x2 + 1 = 0; б) √x + 9 = 0; в) (2x + 1)/(x + 0,5) =0; г) (5x – 4)/((x + 2)(x – 0,8)) = 0.
РЕШЕНИЕ: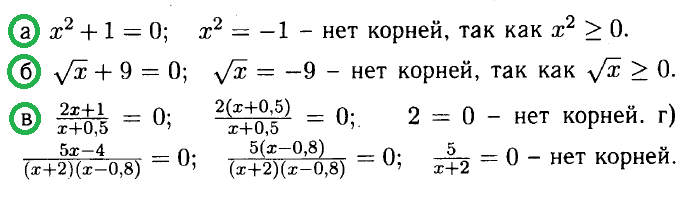
№ 4. Равносильны ли уравнения:
а) 6x – 5 = 0 и 5/6 – х = 0; б) (3х – 12)(√х – 13) = 0 и (х – 169)(√х – 2) = 0; в) √x + 25 = 0 и x2 + 5 = 0?
ОТВЕТЫ: а) да; б) да; в) да.
Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельная С-23 «Уравнения и их корни». Цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой. Цитаты из пособия указаны в учебных целях.
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Макарычев и др.)