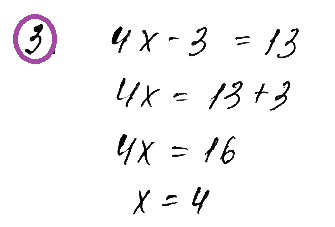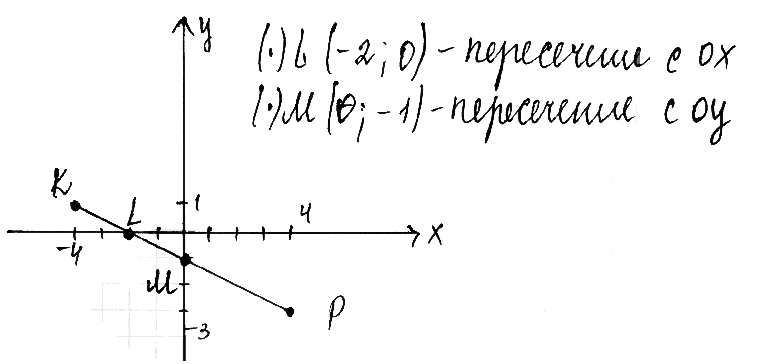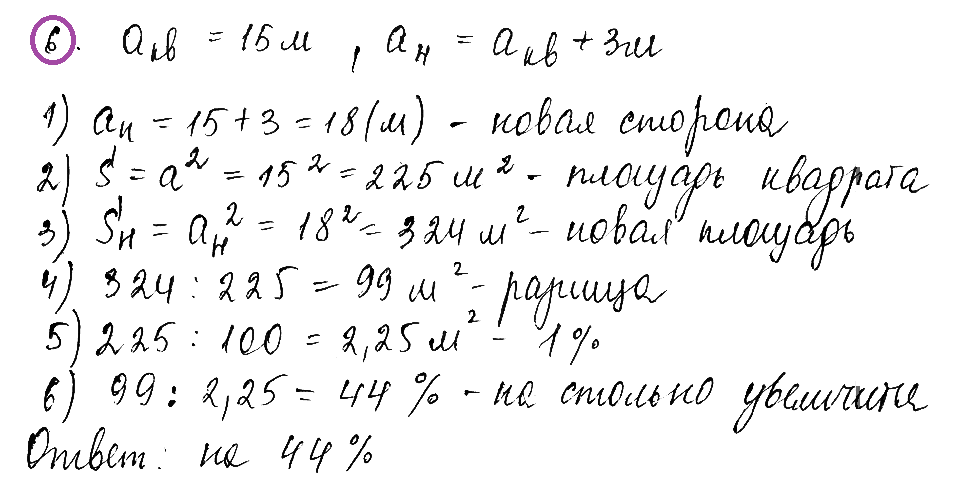Рубрика: Математика

Опубликовано

Математика 5 Виленкин Контрольные

Контрольные работы по математике для 5 класса с ответами по учебнику Виленкина. Цитаты из учебных пособий использованы в учебных целях, а также во избежание редакционных ошибок (в разных изданиях встречаются разные формулировки вопросов).  Математика 5 Виленкин Контрольные + ОТВЕТЫ.

 

Математика 5 класс (Виленкин)
Контрольные работы

 

Уважаемые учителя, родителя и учащиеся на самообучении!

На данной странице идёт обновление учебного материала. Всю информацию о ходе обновления вы найдете в наших пабликах (каналах) соцсетей. Новый материал, подготовленный группой наших учителей, планируется опубликовать в апреле-мае 2023 года. Он будет абсолютно бесплатный и удобный для копирования и размножения в качестве раздаточного материала. Свои пожелания оставляйте также в комментариях ниже.

С уважением, администрация сайта.

 

Примерный перечень тем контрольных работ:

§ 1. Натуральные числа и шкалы 
1. Обозначение натуральных чисел
2. Отрезок. Длина отрезка. Треугольник
3. Плоскость. Прямая. Луч
4. Шкалы и координаты
5. Меньше или больше

§ 2. Сложение и вычитание натуральных чисел 
6. Сложение натуральных чисел и его свойства
7. Вычитание
8. Числовые и буквенные выражения
9. Буквенная запись свойств сложения и вычитания
10. Уравнение

§ 3. Умножение и деление натуральных чисел 
11. Умножение натуральных чисел и его свойства
12. Деление
13. Деление с остатком
14. Упрощение выражений
15. Порядок выполнения действий
16. Степень числа. Квадрат и куб числа

§ 4. Площади и объёмы 
17. Формулы
18. Площадь. Формула площади прямоугольника
19. Единицы измерения площадей
20. Прямоугольный параллелепипед
21. Объёмы. Объём прямоугольного параллелепипеда

§ 5. Обыкновенные дроби
22. Окружность и круг

§ 6. Десятичные дроби.

§ 7. Умножение и деление десятичных дробей 
34. Умножение десятичных дробей на натуральные числа

§ 8. Инструменты для вычислений и измерений
39. Микрокалькулятор
40. Проценты
41. Угол. Прямой и развёрнутый угол. Чертёжный треугольник
42. Измерение углов. Транспортир
43. Круговые диаграммы

 

Математика 5 Виленкин Контрольные работы + ОТВЕТЫ. Цитаты из заданий контрольных работ указаны в учебных целях.

Опубликовано

Математика 5 Мерзляк Тесты

Контрольные тесты для самопроверки по математике в 5 классе с ответами, которые используются в комплекте с учебником «Математика 5 класс» авторов: А.Г. Мерзляк и др. Цитаты из пособия указаны в учебных целях. Математика 5 Мерзляк Тесты + ОТВЕТЫ.

 

Математика 5 класс (Мерзляк)
Контрольные ТЕСТЫ

 

Уважаемые учителя, родителя и учащиеся на самообучении!

На данной странице идёт обновление учебного материала. Всю информацию о ходе обновления вы найдете в наших пабликах (каналах) соцсетей. Новый материал, подготовленный группой наших учителей, планируется опубликовать в апреле-мае 2023 года. Он будет абсолютно бесплатный и удобный для копирования и размножения в качестве раздаточного материала. Свои пожелания оставляйте также в комментариях ниже.

С уважением, администрация сайта.

 

 

Примерный перечень планируемых тестов:

Глава 1. Натуральные числа

  • 1. Ряд натуральных чисел.
  • 2. Цифры. Десятичная запись натуральных чисел.
  • 3. Отрезок. Длина отрезка.
  • 4. Плоскость. Прямая. Луч.
  • 5. Шкала. Координатный луч.
  • 6. Сравнение натуральных чисел.

Глава 2. Сложение и вычитание натуральных чисел

  • 7. Сложение натуральных чисел. Свойства сложения.
  • 8. Вычитание натуральных чисел.
  • 9. Числовые и буквенные выражения. Формулы.
  • 10. Уравнение.
  • 11. Угол. Обозначение углов.
  • 12. Виды углов. Измерение углов.
  • 13. Многоугольники. Равные фигуры.
  • 14. Треугольник и его виды.
  • 15. Прямоугольник. Ось симметрии фигуры.

Глава 3. Умножение и деление натуральных чисел

  • 16. Умножение. Переместительное свойство умножения.
  • 17. Сочетательное и распределительное свойства умножения.
  • 18. Деление.
  • 19. Деление с остатком.
  • 20. Степень числа.
  • 21. Площадь. Площадь прямоугольника.
  • 22. Прямоугольный параллелепипед. Пирамида.
  • 23. Объём прямоугольного параллелепипеда.
  • 24. Комбинаторные задачи.

 

Вы смотрели страницу «Математика 5 Мерзляк Тесты» — контрольные тесты к новому учебнику А.Г. Мерзляк ФГОС.

Опубликовано

Математика 5 Никольский Контрольные

Контрольные работы по математике в 5 классе с ответами к учебнику С. М. Никольского и др. ФГОС. Цитаты из пособия использованы в учебных целях. Математика 5 Никольский Контрольные + ОТВЕТЫ. Работы даются в шести вариантах трёх уровней сложности: варианты А1, А2, Б1, Б2 соответствуют базовому уровню сложности, варианты В1, В2 рассчитаны на учащихся, проявляющих повышенный интерес к математике. Ответы адресованы родителям.

 

Контрольные работы по математике
5 класс (УМК Никольский и др.):

 

Уважаемые учителя, родителя и учащиеся на самообучении!

На данной странице идёт обновление учебного материала. Всю информацию о ходе обновления вы найдете в наших пабликах (каналах) соцсетей. Новый материал, подготовленный группой наших учителей, планируется опубликовать в апреле-мае 2023 года. Он будет абсолютно бесплатный и удобный для копирования и размножения в качестве раздаточного материала. Свои пожелания оставляйте также в комментариях ниже.

С уважением, администрация сайта.

 

Примерный перечень тем учебника для планируемых контрольных работ:

ГЛАВА 1. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ

Ряд натуральных чисел.
Десятичная система записи натуральных чисел.
Сравнение натуральных чисел.
Сложение Законы сложения.
Вычитание.
Решение текстовых задач с помощью сложения и вычитания.
Умножение Законы умножения.
Распределительный закон.
Сложение и вычитание чисел столбиком.
Умножение чисел столбиком.
Степень с натуральным показателем.
Деление нацело.
Решение текстовых задач с помощью умножения и деления.
Задачи «на части».
Деление с остатком.
Числовые выражения.
Задачи на нахождение двух чисел по их сумме и разности.

ГЛАВА 2. ИЗМЕРЕНИЕ ВЕЛИЧИН

Прямая. Луч. Отрезок.
Измерение отрезков.
Метрические единицы длины.
Представление натуральных чисел на координатном луче.
Окружность и круг. Сфера и шар.
Углы. Измерение углов.
Треугольники.
Четырёхугольники.
Площадь прямоугольника. Единицы площади.
Прямоугольный параллелепипед.
Объём прямоугольного параллелепипеда. Единицы объёма.
Единицы массы.
Единицы времени.
Задачи на движение.

ГЛАВА 3. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ

Свойства делимости.
Признаки делимости.
Простые и составные числа.
Делители натурального числа.
Наибольший общий делитель.
Наименьшее общее кратное.

ГЛАВА 4. ОБЫКНОВЕННЫЕ ДРОБИ

Понятие дроби
Равенство дробей
Задачи на дроби
Приведение дробей к общему знаменателю
Сравнение дробей
Сложение дробей
Законы сложения
Вычитание дробей
Умножение дробей
Законы умножения Распределительный закон
Деление дробей
Нахождение части целого и целого по его части
Задачи на совместную работу
Понятие смешанной дроби
Сложение смешанных дробей
Вычитание смешанных дробей.
Умножение и деление смешанных дробей.
Представление дробей на координатном луче.
Площадь прямоугольника. Объём прямоугольного параллелепипеда.

 

Работы предназначены для проверки знаний учащихся по всем темам, изучаемым в 5 классе. А также ориентированы на работу с любым учебником по математике из Федерального перечня учебников. Проверочные работы помогут оперативно выявить пробелы в знаниях, адресованы как учителям математики, так и учащимся для самоконтроля. Ответы даются только для родителей.

Вы смотрели: Математика 5 Никольский Контрольные работы по математике в 5 классе с ответами к учебнику С. М. Никольского и др. ФГОС (к новому учебнику).

 

Опубликовано

Математика 6 Итоговая контрольная В4

Итоговая контрольная работа по математике за 6 класс с ответами  и решениями (вариант 4-й из 4-х) для любого УМК. Математика 6 Итоговая контрольная В4 + ОТВЕТЫ. Можно использовать в комплекте с любым учебником по математике 6 класса общеобразовательных учреждений.

 

Математика 6 класс (любой УМК)
ОТВЕТЫ на контрольную. Вариант 4

Ещё варианты: ИКР Вариант 1 ИКР Вариант 2 ИКР Вариант 3

 

№ 1. Выполните действия: 2 1/12 : (1 5/9 – 1/6) – 3,3.
ОТВЕТ: –1,8.
Решение:

№ 2. Расстояние между поселками равно 126 км. За первый час автобус проехал 4/9 этого расстояния. Сколько километров осталось проехать автобусу?
ОТВЕТ: 70 км.
Решение:

№ 3. Решите уравнение 9 – 2х = 1.
ОТВЕТ: 4.
Решение:

№ 4. Постройте отрезок АВ, где А(–3; –2), В(2; 3). Запишите координаты точек пересечения его с осями координат.
ОТВЕТ: (–1; 0), (0; 1).

№ 5. В школьную столовую привезли апельсиновый и лимонный соки. Количество лимонного сока составляет 3/8 количества всего сока. Апельсинового сока привезли на 10 литров больше, чем лимонного. Сколько сока привезли в столовую?
ОТВЕТ: 40 л.

№ 6. Сторона квадрата равна 20 см. На сколько процентов уменьшится его площадь, если сторону уменьшить на 2 см?
ОТВЕТ: на 19 %.

 

Вы смотрели: Итоговую контрольную работу по математике за 6 класс с ответами  и решениями (вариант 4 из 4-х) для любого УМК. Математика 6 Итоговая контрольная В4 + ОТВЕТЫ. Ответы даны для учителей и родителей с целью проверки правильности выполнения заданий.

Ещё варианты: [ИКР Вариант 1 ИКР Вариант 2 ИКР Вариант 3

Опубликовано

Математика 6 Итоговая контрольная В3

Итоговая контрольная работа по математике за 6 класс с ответами  и решениями (вариант 3-й из 4-х) для любого УМК. Математика 6 Итоговая контрольная В3 + ОТВЕТЫ. Можно использовать в комплекте с любым учебником по математике 6 класса общеобразовательных учреждений.

 

Математика 6 класс (любой УМК)
ОТВЕТЫ на контрольную. Вариант 3

Ещё варианты: ИКР Вариант 1 ИКР Вариант 2 ИКР Вариант 4

 

№ 1. Выполните действия: 1,4 – 1 1/2 • (1 2/5 + 1/5).
ОТВЕТ: –1.
Решение:

№ 2. Фермер имеет 168 гектаров земли. Из них 5/12 он выделил для выпаса скота. Сколько земли он оставил для других дел?
ОТВЕТ: 98 га.
Решение:

№ 3. Решите уравнение 4х – 3 = 13.
ОТВЕТ: 4.
Решение:

№ 4. Постройте отрезок КР, где К(–4; 1), Р(4; –3). Запишите координаты точек пересечения его с осями координат.
ОТВЕТ: (–2; 0), (0; –1).

№ 5. На соревнованиях по лыжам шестиклассники бежали дистанции в 3 км и 2 км. На длинной дистанции выступило 2/5 числа всех шестиклассников. Короткую дистанцию бежали на 16 человек больше, чем длинную. Сколько шестиклассников участвовали в соревнованиях?
ОТВЕТ: 80 шестиклассников.

№ 6. Сторона квадрата равна 15 м. На сколько процентов увеличится его площадь, если сторону увеличить на 3 м?
ОТВЕТ: на 44 %.

 

Вы смотрели: Итоговую контрольную работу по математике за 6 класс с ответами  и решениями (вариант 3 из 4-х) для любого УМК. Математика 6 Итоговая контрольная В3 + ОТВЕТЫ. Ответы даны для учителей и родителей с целью проверки правильности выполнения заданий.

Ещё варианты: ИКР Вариант 1 ИКР Вариант 2 ИКР Вариант 4

Опубликовано

Математика 6 Итоговая контрольная В2

Итоговая контрольная работа по математике за 6 класс с ответами  и решениями (вариант 2-й из 4-х) для любого УМК. Математика 6 Итоговая контрольная В2 + ОТВЕТЫ. Можно использовать в комплекте с любым учебником по математике 6 класса общеобразовательных учреждений.

 

Математика 6 класс (любой УМК)
ОТВЕТЫ на контрольную. Вариант 2

Ещё варианты: ИКР Вариант 1 ИКР Вариант 3 ИКР Вариант 4

 

№ 1. Выполните действия: (–1 1/9) • (1 3/5 – 1/4) + 2,5.
ОТВЕТ: 1.
Решение:

№ 2. Колхоз собрал 552 т сахарной свеклы. На сахарный завод вывезли 23/24 собранного урожая. Сколько тонн сахарной свеклы осталось вывезти?
ОТВЕТ: 23 т.
Решение:

№ 3. Решите уравнение 8 + 5х = 23.
ОТВЕТ: 3.
Решение:

№ 4. Постройте отрезок ВС, где В(–2; –5), С(4; 1). Запишите координаты точек пересечения его с осями координат.
ОТВЕТ: (3; 0), (0; –3).

№ 5. В шестом классе одиннадцатилетних учеников на 4 больше, чем двенадцатилетних. Число одиннадцатилетних учеников составляет 4/7 числа всех шестиклассников. Сколько учеников в таком классе?
ОТВЕТ: 28 учеников.

№ 6. Длина прямоугольника равна 15 м, а ширина 8 м. На сколько процентов увеличится его площадь, если ширину увеличить на 6 м?
ОТВЕТ: на 75%.

 

Вы смотрели: Итоговую контрольную работу по математике за 6 класс с ответами  и решениями (вариант 2 из 4-х) для любого УМК. Математика 6 Итоговая контрольная В2 + ОТВЕТЫ. Ответы даны для учителей и родителей с целью проверки правильности выполнения заданий.

Ещё варианты: ИКР Вариант 1 ИКР Вариант 3 ИКР Вариант 4

Опубликовано

Мерзляк 6 класс Контрольные работы

Мерзляк 6 класс Контрольные работы по математике в четырех вариантах для УМК Мерзляк, Полонский, Якир.

Цитаты из пособия «Математика 6 класс. Методическое пособие / Е.В. Буцко и др. — М.: Вентана-Граф» использованы в учебных целях.

 

Математика 6 класс (УМК Мерзляк)
Контрольные работы (4 варианта):

 

К-1 «Делимость натуральных чисел» + ОТВЕТЫ на вариант 1.

Контрольная работа № 1

К-2 «Сравнение, сложение и вычитание дробей » + ОТВЕТЫ на все варианты.

Контрольная работа № 2

К-3 «Умножение дробей» + ОТВЕТЫ на все варианты

Контрольная работа № 3

К-4 «Деление дробей» + ОТВЕТЫ на все варианты

Контрольная работа № 4

К-5 «Отношения и пропорции. Процентное отношение двух чисел» + ОТВЕТЫ на все варианты

Контрольная № 5 с ответами

К-6 «Прямая и обратная пропорциональные зависимости. Окружность и круг. Вероятность случайного события» + ОТВЕТЫ на все варианты

Контрольная № 6 с ответами

К-7 «Рациональные числа. Сравнение рациональных чисел» + ОТВЕТЫ на все варианты

Контрольная работа № 7

К-8 «Сложение и вычитание рациональных чисел» + ОТВЕТЫ на вариант 1

Контрольная работа № 8

К-9 «Умножение и деление рациональных чисел» + ОТВЕТЫ на все варианты

К-9 Варианты 1-2 К-9 Варианты 3-4

К-10 «Решение уравнений и решение задач с помощью уравнений» + ОТВЕТЫ на все варианты

К-10 Варианты 1-2 К-10 Варианты 3-4

К-11 «Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость» + ОТВЕТЫ на все варианты

К-11 Вариант 1 К-11 Вариант 2 К-11 Вариант 3 К-11 Вариант 4

К-12 «Итоговая контрольная работа за 6 класс» + ОТВЕТЫ на все варианты

К-12 Вариант 1 К-12 Вариант 2 К-12 Вариант 3 К-12 Вариант 4

 

12 контрольных работ в соответствии с календарным планированием. Каждая работа содержит 4 варианта. Такой обширный материал поможет учителю организовать объективный и эффективный контроль знаний.
Адресовано учителям, работающим по учебнику «Математика. 6 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.

Вы смотрели: Мерзляк 6 класс Контрольные работы по математике в четырех вариантах УМК Мерзляк, Полонский, Якир.

Смотрите также аналогичные контрольные работы из Дидактических материалов для УМК Мерзляк (2 варианта с ответами)

 

Опубликовано

Мерзляк 5 класс Контрольные работы

Мерзляк 5 класс Контрольные работы по математике с ответами в четырех вариантах УМК Мерзляк, Полонский, Якир. Цитаты из пособия «Математика 5 класс. Методическое пособие / Е.В. Буцко и др. — М.: Вентана-Граф» использованы в учебных целях.

 

Математика 5 класс (Мерзляк)
Контрольные работы:

К-1 «Линейные уравнения с одной переменной» + ОТВЕТЫ

Контрольная работа № 1

К-2 «Сложение и вычитание натуральных чисел. Числовые и буквенные выражения. Формулы» + ОТВЕТЫ

Контрольная работа № 2

 

К-3 «Уравнение. Угол. Многоугольники» + ОТВЕТЫ

Контрольная работа № 3

К-4 «Умножение и деление натуральных чисел. Свойства умножения» + ОТВЕТЫ

Контрольная работа № 4

К-5 «Деление с остатком. Площадь прямоугольника. Прямоугольный параллелепипед и его объём. Комбинаторные задачи» + ОТВЕТЫ

Контрольная работа № 5

К-6 «Обыкновенные дроби» + ОТВЕТЫ

Контрольная работа № 6

К-7 «Понятие о десятичной дроби. Сравнение, округление, сложение и вычитание десятичных дробей» + ОТВЕТЫ

К-7 Варианты 1-2 К-7 Варианты 3-4

К-8 «Умножение и деление десятичных дробей» + ОТВЕТЫ

К-8 Варианты 1-2 К-8 Варианты 3-4

К-9 «Среднее арифметическое. Проценты» + ОТВЕТЫ

К-9 Варианты 1-2 К-9 Варианты 3-4

К-10 «Итоговая контрольная работа за 5 класс» + ОТВЕТЫ

К-10 Варианты 1-2 КР-10 Варианты 3-4

 

10 контрольных работ в соответствии с календарным планированием. Каждая работа содержит 4 варианта. Такой обширный материал поможет учителю организовать объективный и эффективный контроль знаний.
Адресовано учителям, работающим по учебнику «Математика. 5 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.

 

Вы смотрели: Мерзляк 5 класс Контрольные работы по математике в четырех вариантах с решениями для УМК Мерзляк из Методического пособия Буцко.

Смотрите также 10 аналогичных контрольных работ из Дидактических материалов для 5 класса (в 2-х вариантах)

 

Опубликовано

Математика 6 Козлова Контрольные

Математика 6 Козлова Контрольные работы с ответами (4 варианта). Цитаты из пособия для учащихся «Контрольные работы по математике. 6 класс / С.А. Козлова, А.Г. Рубин — М.: Баласс», которое используется в комплекте с учебником «Математика 6 класс» авторов С.А.Козловой, А.Г.Рубина. Цитаты из пособия указаны в учебных целях, при постоянном использовании контрольных работ в 6 классе рекомендуем купить книгу: Козлова, Рубин: Контрольные работы к учебнику «Математика», 6 класс.

Контрольные работы по математике
6 класс (УМК Козлова, Рубин)

Контрольная № 1 + Ответы К-1 «Обыкновенные дроби»

Контрольная № 2 + Ответы К-2 «Десятичные дроби»

Контрольная № 3 + Ответы К-3 «Элементы геометрии»

Контрольная работа № 4 К-4 «Пропорции»

Контрольная № 5 + Ответы К-5 «Проценты»

 

Готовятся к публикации:

К-6 «Целые числа»

К-7 «Рациональные числа»

К-8 «Понятие о действительных числах»

К-9 «Геометрические и комбинаторные задачи»

К-10 Итоговая контрольная работа за курс 6 класс

 

Каждая из контрольных работ, включая четвертные и годовую, содержит 6 заданий и рассчитана на один урок (40-45 мин.). При этом каждая работа состоит из двух частей: обязательной и дополнительной.

Задания обязательной части (в каждой из контрольных работ это первые четыре задания) относятся к необходимому уровню.
Задания дополнительной части (в каждой из контрольных работ это последние два задания), в свою очередь, относятся к двум уровням: повышенному (задание № 5) и максимальному (задание № 6).

Эти уровни подробно обсуждаются в предисловии к учебнику и ещё подробнее в методических рекомендациях для учителя. Кратко их можно охарактеризовать следующим образом. К необходимому уровню относятся задания, позволяющие выяснить, насколько ученик овладел знаниями на уровне стандарта. К повышенному уровню относятся задания, позволяющие отследить, насколько ученик овладел знаниями на уровне авторской программы. Максимальный уровень соответствует требованиям, превышающим как требования стандарта, так и требования авторской программы, и предполагает высокую степень самостоятельности мышления учащихся. Он содержит задания креативного характера, позволяющие определить, насколько ученик может самостоятельно применять имеющиеся у него знания в нестандартных ситуациях, в необычных обстоятельствах, не описанных подробно в учебниках и не отработанных на занятиях.

Задания, в той или иной мере похожие на задание № 5, встречались на страницах учебника ранее, и ребята по желанию могли потренироваться в их решении. Задание № 6 не имеет полных аналогов в учебнике, но тем не менее его можно выполнить, творчески освоив материалы учебника.

Дополнительная часть каждой контрольной работы предназначена только для желающих. Выполнение дополнительной части оценивается только отметкой «4» или «5» (в противном случае учитель пишет на работе «Без отметки»). При этом отметка «4» выставляется в журнал только по желанию учащегося.

 

Вы смотрели: Математика 6 Козлова Контрольные работы с ответами (4 варианта). Цитаты из пособия для учащихся «Контрольные работы по математике. 6 класс / С.А. Козлова, А.Г. Рубин — М.: Баласс», которое используется в комплекте с учебником «Математика 6 класс» авторов С.А.Козловой, А.Г.Рубина.

 

Опубликовано

Самостоятельные работы Математика 5 Мерзляк

Самостоятельные работы Математика 5 Мерзляк — это цитаты самостоятельных работ из пособия для учащихся «Математика 5 класс. Дидактические материалы / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир — М.: Вентана-Граф» (Алгоритм успеха), которое используется в комплекте с учебником «Математика 5 класс» авторов: Мерзляк и др. Цитаты из пособия указаны в учебных целях. При постоянном использовании самостоятельных работ в 5 классе рекомендуем купить книгу:  Мерзляк, Рабинович, Полонский: Математика. 5 класс. Дидактические материалы. ФГОС.

 

Самостоятельные работы по математике
(УМК Мерзляк) 5 класс

СР-1. Упражнения для повторения материала 1–4 классов + Ответы на все варианты

Самостоятельная № 01

СР-2. Ряд натуральных чисел. Десятичная запись натуральных чисел + Ответы на все варианты

Самостоятельная № 02

СР-3. Отрезок. Длина отрезка + Ответы на все варианты

Самостоятельная № 03

СР-4. Прямая. Луч. Шкала. Координатный луч + Ответы на все варианты

Самостоятельная № 04

СР-5. Сравнение натуральных чисел + Ответы на все варианты

СР-05 Варианты 1-2  СР-05 Варианты 3-4

СР-6. Сложение натуральных чисел. Свойства сложения + Ответы на все варианты

СР-06 Варианты 1-2  СР-06 Варианты 3-4

СР-7. Вычитание натуральных чисел + Ответы на все варианты

СР-07 Варианты 1-2  СР-07 Варианты 3-4

СР-8. Числовые и буквенные выражения–формулы (1 часть) + Ответы на все варианты

СР-08 Варианты 1-2  СР-08 Варианты 3-4

СР-9. Числовые и буквенные выражения–формулы (2 часть)

СР-09 Варианты 1-2  СР-09 Варианты 3-4

СР-10. Уравнение

СР-10 Варианты 1-2  СР-10 Варианты 3-4

СР-11. Угол. Обозначение углов

Самостоятельная № 11

СР-12. Виды углов. Измерение углов

СР-12. Многоугольники. Равные фигуры

СР-13. Треугольник и его виды

СР-15 Умножение

СР-16. Сочетательное и распределительное свойства умножения

СР-17. Деление

СР-18. Деление с остатком

СР-19. Степень числа

СР-20. Площадь. Площадь прямоугольника

СР-21. Прямоугольный параллелепипед. Пирамида

СР-22. Объём прямоугольного параллелепипеда

СР-23. Комбинаторные задачи

СР-24. Понятие обыкновенной дроби

СР-25. Правильные и неправильные дроби. Сравнение дробей + Ответы на вариант 1

Самостоятельная № 25

СР-26. Сложение и вычитание дробей с одинаковыми знаменателями + Ответы на вариант 1

Самостоятельная № 26

СР-27. Дроби и деление натуральных чисел. Смешанные числа

СР-28. Представление о десятичных дробях

СР-29. Сравнение десятичных дробей

СР-30. Округление чисел

СР-31. Сложение и вычитание десятичных дробей

СР-32. Умножение десятичных дробей

СР-33. Деление десятичных дробей

СР-34. Среднее арифметическое. Среднее значение величины

СР-35. Проценты. Нахождение процентов от числа

СР-36. Нахождение числа по его процентам

 

Вы смотрели «Самостоятельные работы Математика 5 Мерзляк». Цитаты самостоятельных работ из пособия для учащихся «Математика 5 класс. Дидактические материалы / А.Г. Мерзляк и др.» (Алгоритм успеха).