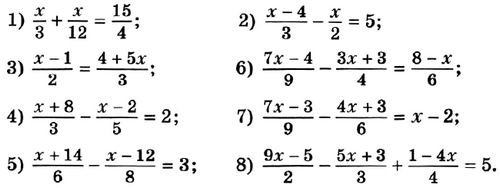Самостоятельная работа № 13 по алгебре в 7 классе «Умножение многочленов на многочлен» с ответами (Вариант 3). Дидактические материалы (упражнения №№ 103 — 110) для учителей, учащихся и родителей. Алгебра 7 Мерзляк С-13 В3.
Вернуться к Списку самостоятельных работ
Алгебра 7 класс (Мерзляк)
Самостоятельная работа № 13.
Вариант 3
Алгебра 7 Мерзляк С-13 В3
ОТВЕТЫ на самостоятельную работу:
№ 103. Преобразуйте в многочлен стандартного вида выражение:
1) (х + 5)(y – 7);
2) (х – 1)(х + 5);
3) (3х – 5)(2х + 7);
4) (5x2 – 1)(5х + 1);
5) (5m – 2n)(3m + n);
6) (4x2 – х)(2x2 + 3х);
7) (–2 – у)(y2 + 3);
8) (3a2 – b)(4a2 + 3b);
9) (а – 3)(a2 + 4а + 2);
10) (у – 2z)(y2 – 2yz – 5z2);
11) m(2m – 1)(3m + 2);
12) –6x2(4 – 2х)(3x2 + 11х).
№ 104. Упростите выражение:
1) (х + 3)(х – 7) – 4х(5 – 2х);
2) (х + 2)(у – 6) + (y + 3)(у – 4);
3) (х – 3)(3х + 1) – (2х + 3)(4х – 1);
4) (2а – 3b)(7а + 4b) – (3,5а + b)(4а – 6b);
5) (m3 – 3n)(m2 + 2n) – 4m3(m2 + 7n).
№ 105. Решите уравнение:
1) (х – 4)(х + 2) – (х – 5)(х + 6) = –х;
2) 12х2 – (3х – 4)(4х + 1) = 19;
3) (3х + 5)(2х + 1) = (6х + 5)(х – 3) + 7;
4) (х + 1)(х – 2) – (х + 5)(х + 4) = –2.
№ 106. Упростите выражение и найдите его значение:
1) (х + 7)(х – 3) – (х – 6)(х + 2), если х = –2,5;
2) (а + 3)(а – 6) + (9 – 5а)(а + 1), если a = 1 1/4.
№ 107. Докажите, что при любом значении переменной значение выражения (х + 1)(x2 + х – 4) – (х + 2)(x2 – 3) равно 2.
№ 108. Докажите, что значение выражения (n – 5)(n + 5) – {n – 2)(n – 12) кратно 7 при всех натуральных значениях п.
№ 109. Найдите четыре последовательных натуральных числа таких, что произведение второго и четвёртого из этих чисел на 45 больше произведения первого и третьего.
ОТВЕТ: 21, 22, 23, 24.
№ 110. Длина прямоугольника на 3 см больше его ширины. Если длину уменьшить на 2 см, а ширину увеличить на 5 см, то площадь прямоугольника увеличится на 14 см2. Найдите исходные длину и ширину прямоугольника.
ОТВЕТ: 3 см, 6 см.
Вы смотрели: Самостоятельная работа по алгебре в 7 классе «Умножение многочленов на многочлен» с ответами. Дидактические материалы для учителей, учащихся и родителей. Алгебра 7 Мерзляк С-13 В3.
Другие варианты: С-13. Вариант 1 С-13. Вариант 2
Вернуться к Списку самостоятельных работ по алгебре в 7 классе УМК Мерзляк.
Перейти к Списку контрольных работ по алгебре в 7 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Дидактические материалы. Алгебра 7 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.

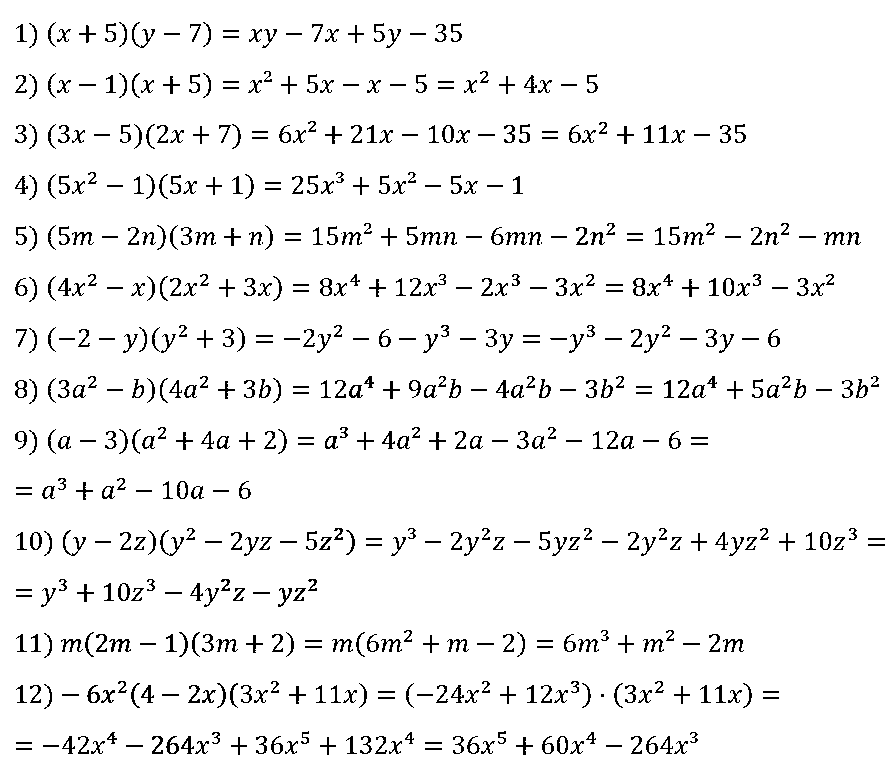
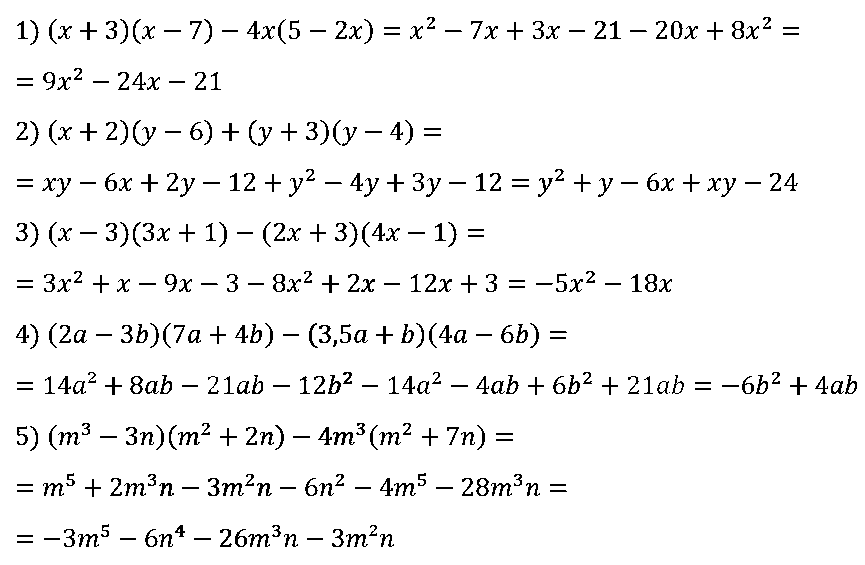

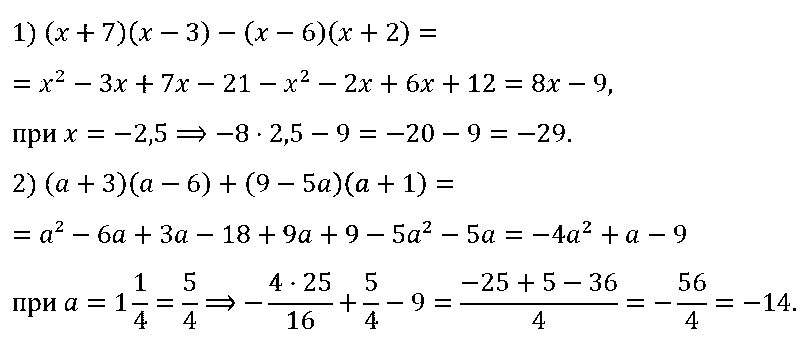
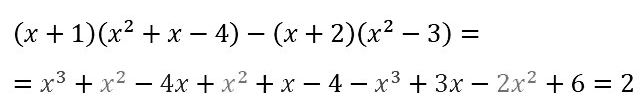
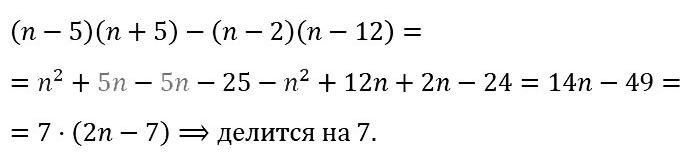
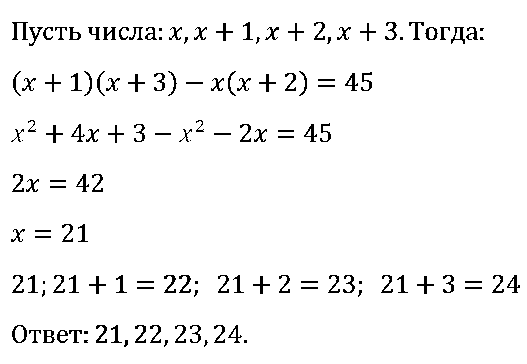



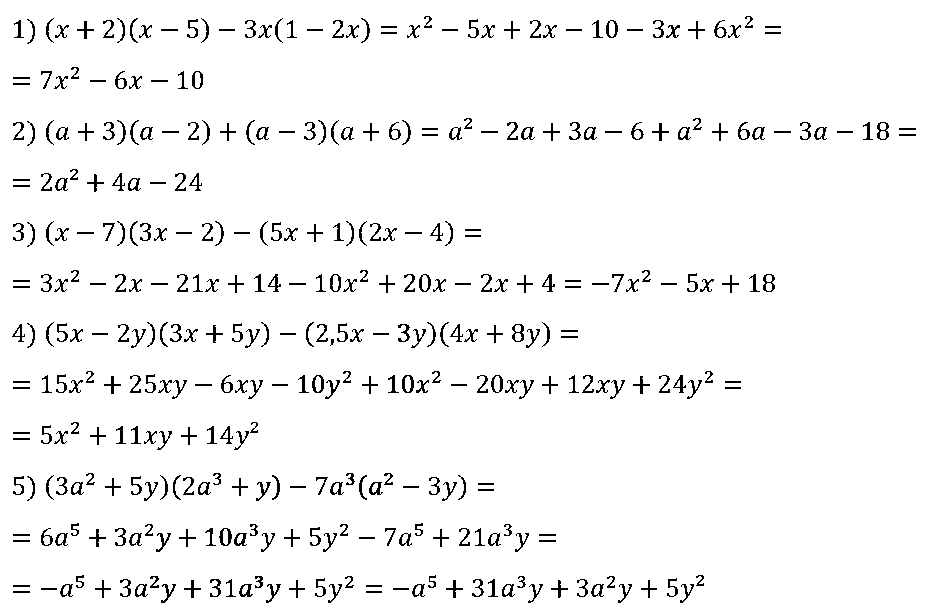

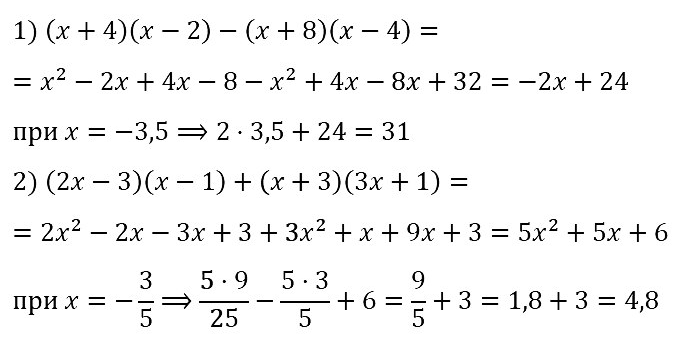
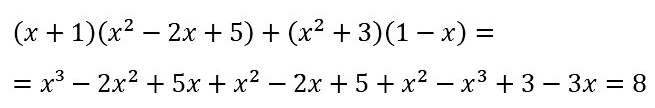
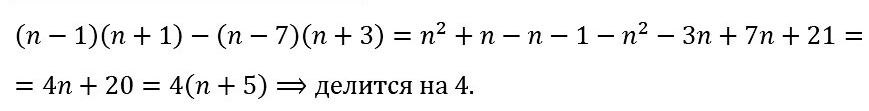
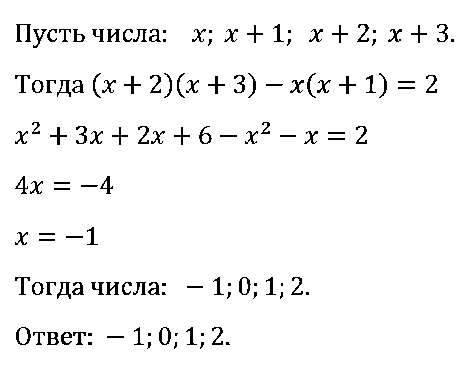


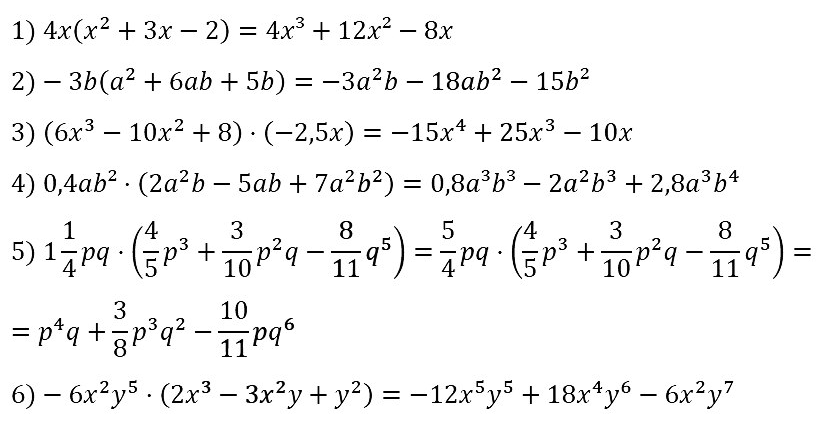
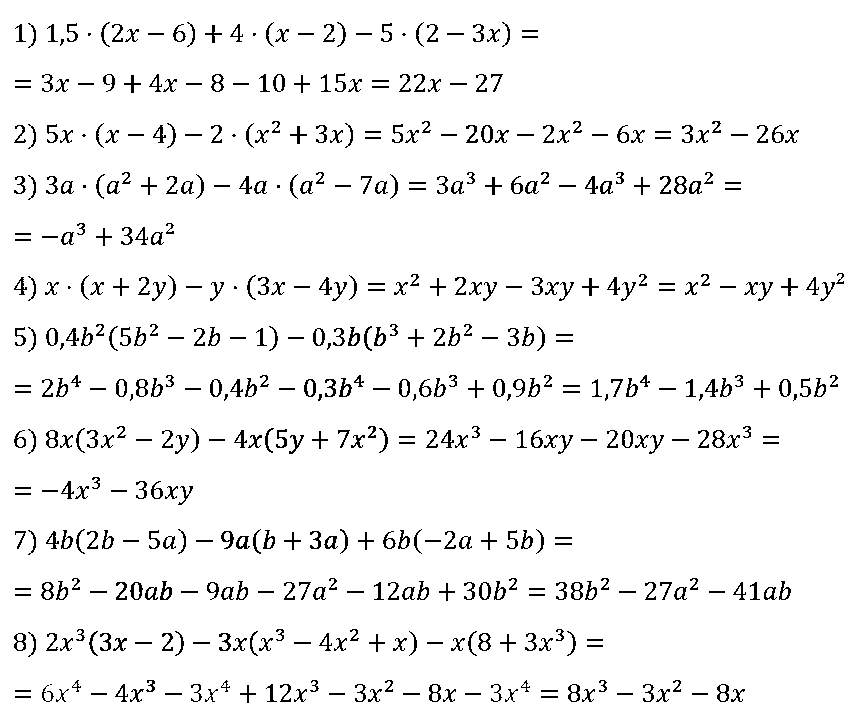
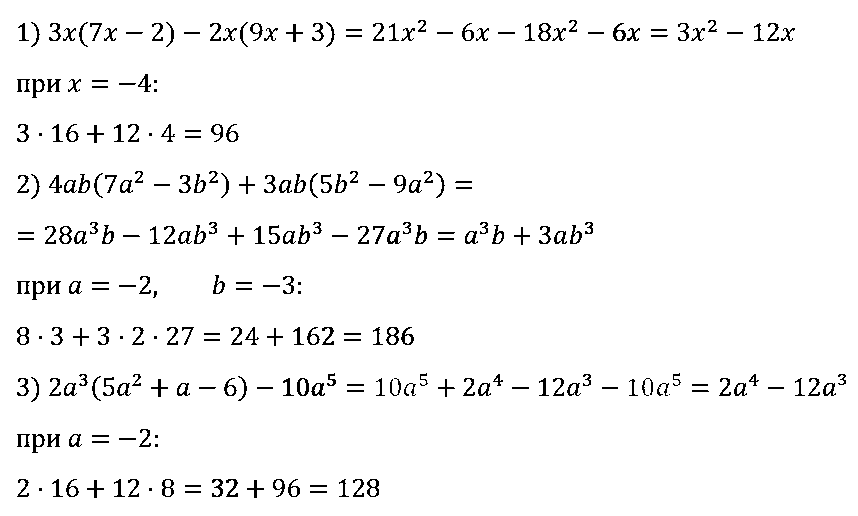
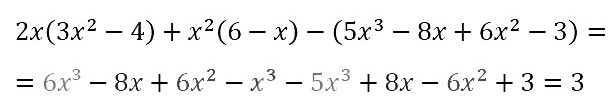
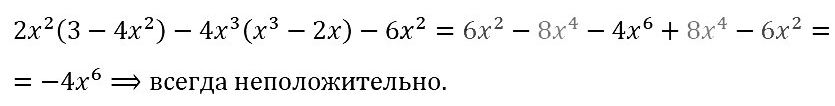
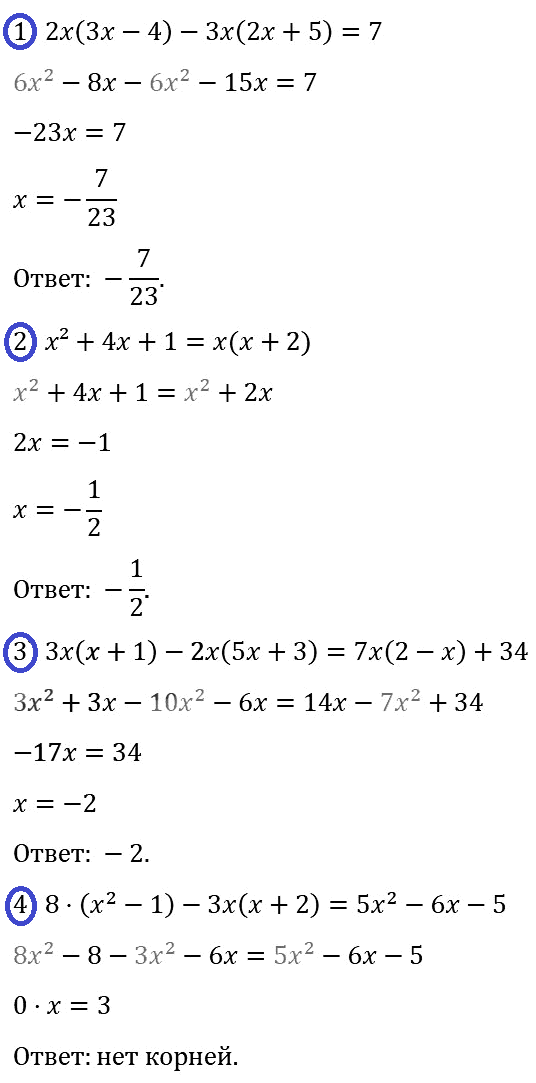
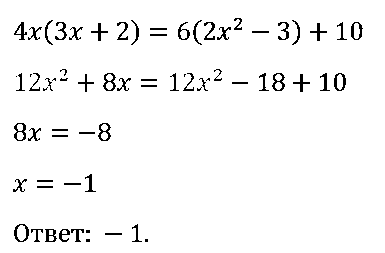
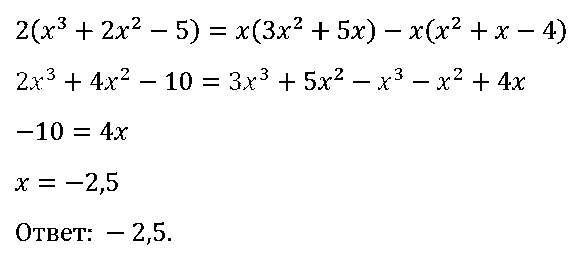
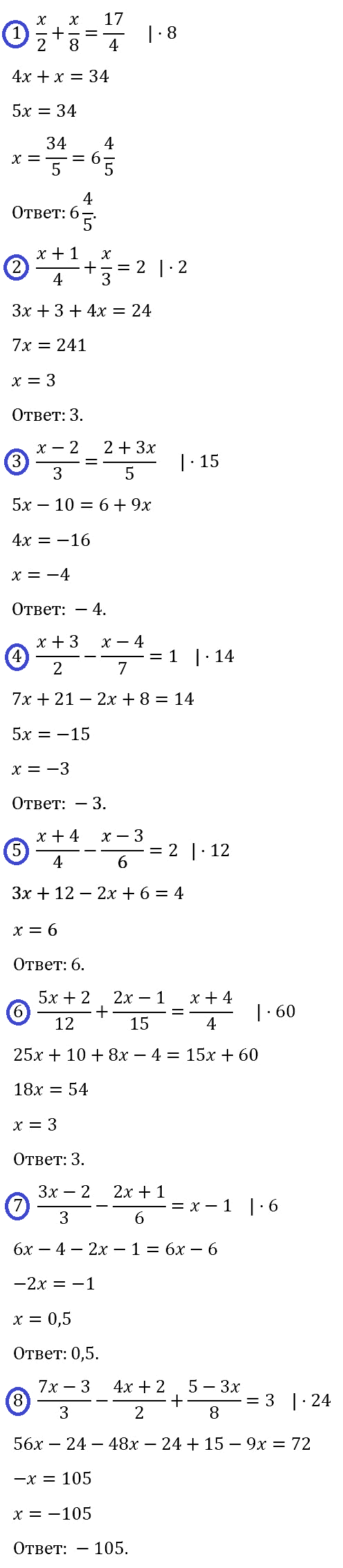



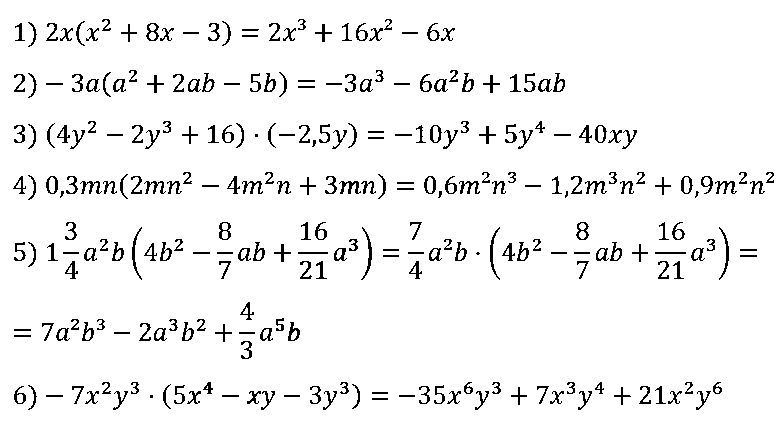
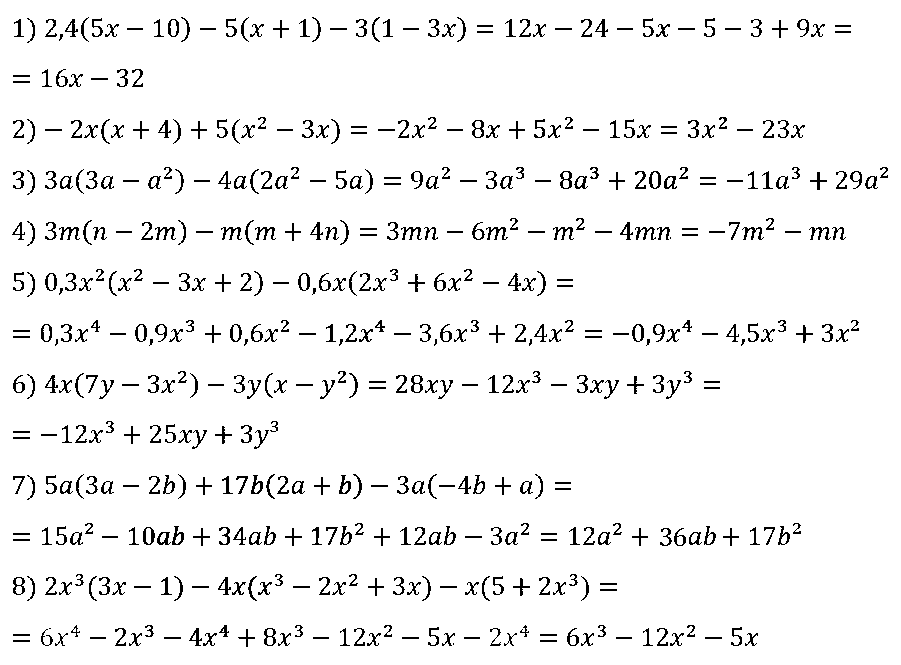
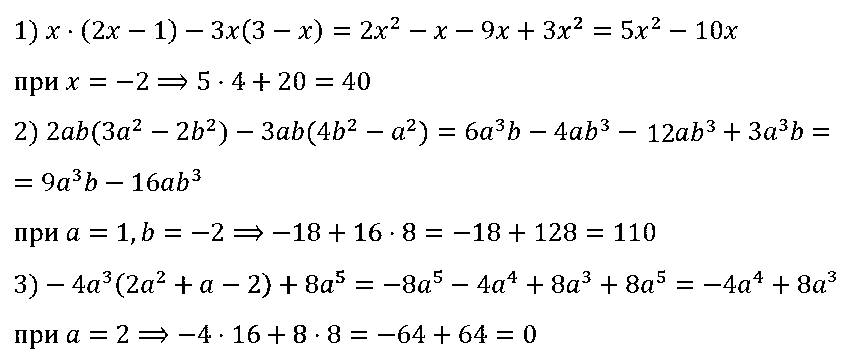
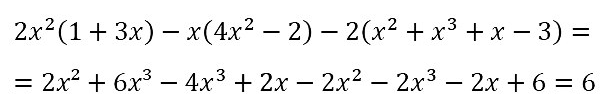
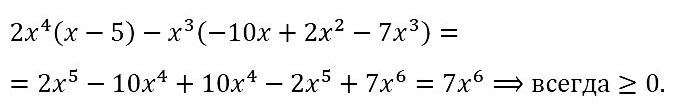
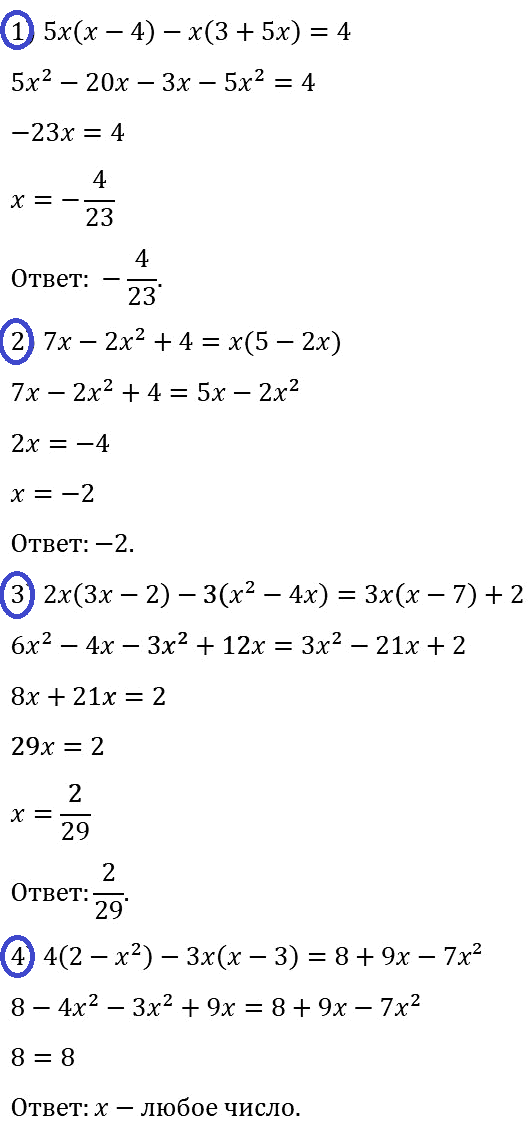
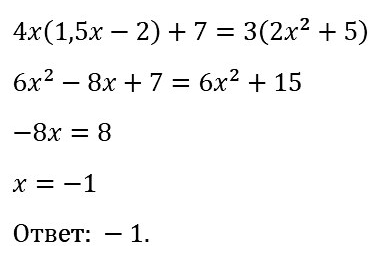
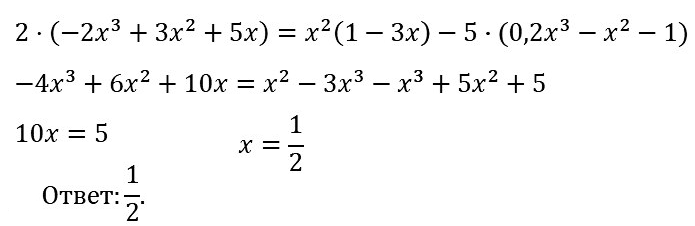



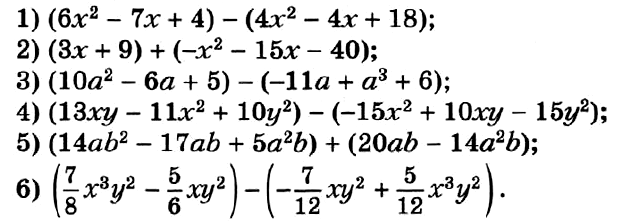 № 77. Докажите тождество:
№ 77. Докажите тождество:

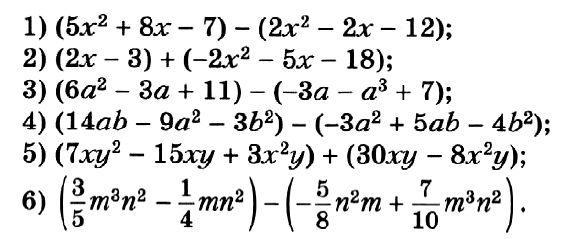 № 77. Докажите тождество:
№ 77. Докажите тождество:


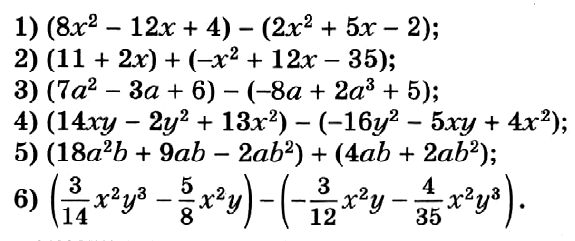 № 77. Докажите тождество:
№ 77. Докажите тождество: