Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы» с ответами для УМК Мерзляк, Полонский, Якир в 4-х вариантах.
Вернуться к Списку контрольных работ
Геометрия 9 класс (УМК Мерзляк)
Контрольная работа № 4
Тема: Векторы
К-4 Варианты 1, 2 (задания)
К-4 Варианты 3, 4 (задания)
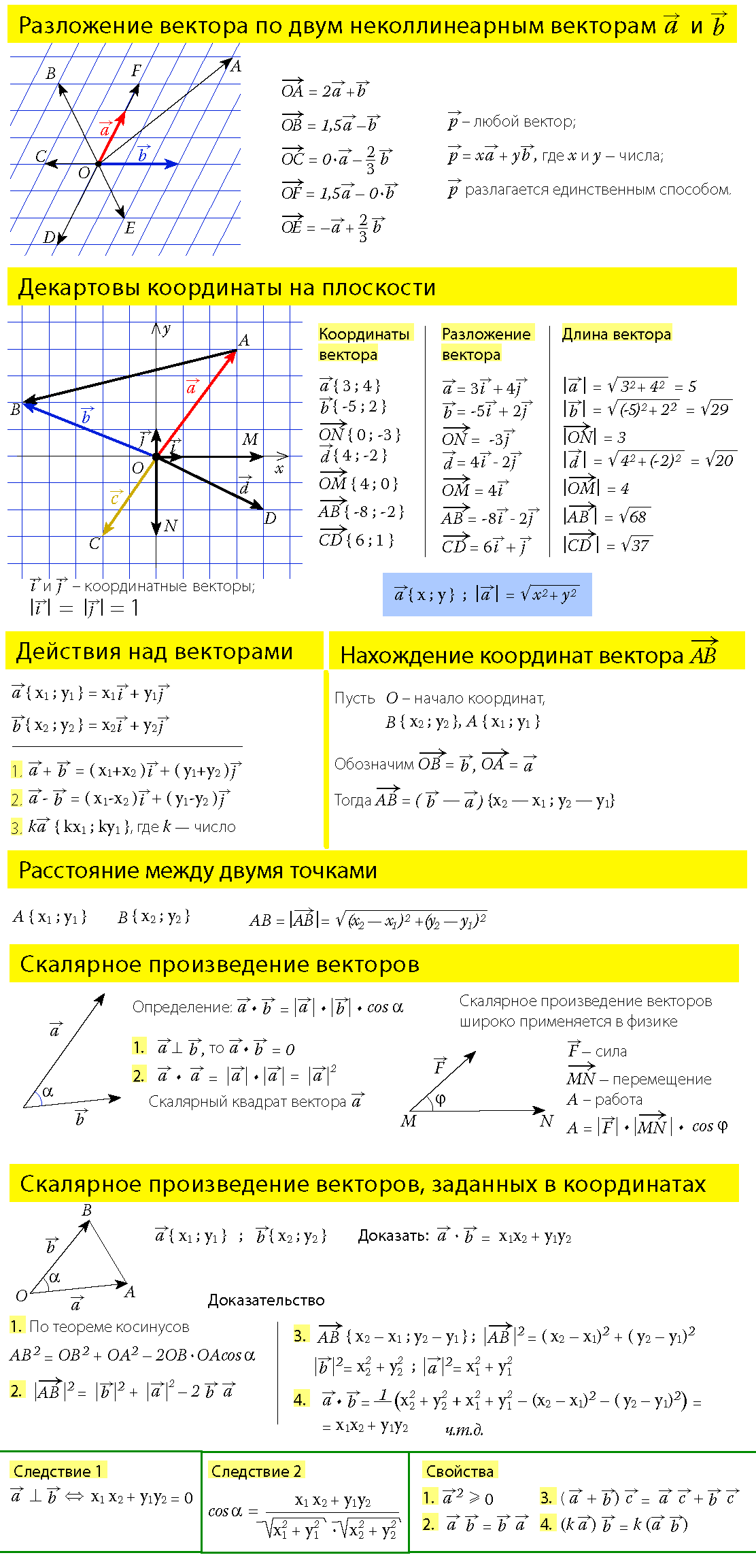
Справочный материал по теме «Векторы»
ОТВЕТЫ на Вариант 1
№ 1. Даны точки A (–3; 1), B (1; –2) и C (–1; 0). Найдите:
1) координаты векторов AB и AC;
2) модули векторов AB и AC;
3) координаты вектора MK = 2AB – 3AC;
4) скалярное произведение векторов AB и AC;
5) косинус угла между векторами AB и AC.
ОТВЕТЫ: 1) АВ (4; –3); AC (2; –1);
2) |AB| = √[16+9] = 5; |AC| = √[4+1] = √5;
3) MK = 2AB – 3AC = (8–6; –6+3) = (2; –3);
4) AB • AC = 4 • 2 + 3• 1 = 11;
5) cos a = (AB • AC) / (|AB| • |AC|) = 11/(5√5) = 0,9839 (а = 10,3°).
№ 2. Начертите треугольник ABC. Постройте вектор:
1) AB + BC; 2) AC – AB; 3) CA + CB.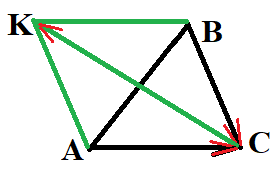
ОТВЕТ: 1) AB + BC = AC; 2) AC – AB = BC; 3) CA + CB = CK.
№ 3. Даны векторы m (4; 14) и n (–7; k). При каком значении k векторы m и n: 1) коллинеарны; 2) перпендикулярны?
ОТВЕТ: 1) при k = –49/2; 2) при k = 2.
№ 4. На сторонах BC и CD параллелограмма ABCD отмечены соответственно точки M и P так, что BM : MC = 2 : 5, CP : PD = 3 : 1. Выразите вектор MP через векторы AB = а и AD = b.
ОТВЕТ: МР = МС + СР = 5/7 • b + (–3/4 • а).
№ 5. Найдите косинус угла между векторами а = 4m – p и b = m + 2p, если m ⊥ p и m = |p| = 1.
ОТВЕТ: cos ∠(a, b) = 2/√85 = 2√85/85 (≈ 0,217).
ОТВЕТЫ на Вариант 2
№ 1. Даны точки A (2; –1), C (3; 2) и D (–3; 1). Найдите:
1) координаты векторов AC и AD;
2) модули векторов AC и AD;
3) координаты вектора EF = 3AC – 2AD;
4) скалярное произведение векторов AC и AD;
5) косинус угла между векторами AC и AD.
ОТВЕТЫ: 1) АC (1; 3); AD (–5; 2);
2) |AC| = √[1+9] = √10; |AD| = √[25+4] = √29;
3) EF = 3AC – 2AD = (3+10; 9–4) = (13; 5);
4) AC • AD = 1 • (–5) + 3 • 2 = 1;
5) cos a = (AC • AD) / (|AC| • |AD|) = 1 / (√10 • √29) = 0,058722 (а = 86,63°).
№ 2. Начертите треугольник ABC. Постройте вектор:
1) AC + CB; 2) BA – BC; 3) AC + AB.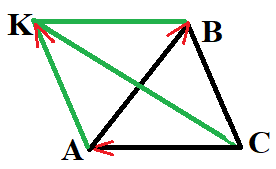
ОТВЕТ: 1) AC + CB = АВ; 2) BA – BC = СА; 3) AC + AB = АК.
№ 3. Даны векторы а (3; –4) и b (m; 9). При каком значении m векторы а и b: 1) коллинеарны; 2) перпендикулярны?
ОТВЕТ: 1) m = –6 3/4; 2) m = 12.
№ 4. На сторонах AB и BC параллелограмма ABCD отмечены соответственно точки M и K так, что AM : MB = 3 : 4, BK : KC = 2 : 3. Выразите вектор MK через векторы DA = а и DC = b.
ОТВЕТ: MK = MB + BK = 4/7 • b – 2/5 • a.
№ 5. Найдите косинус угла между векторами m = 5а + b и n = 2а – b, если a ⊥ b и |a| = |b| = 1.
ОТВЕТ: cos ∠(m, n) = 9/√130 = 9√130/130 (≈ 0,789).
ОТВЕТЫ на Вариант 3
№ 1. Даны точки A (3; –2), B (1; –1) и C (–1; 1). Найдите:
1) координаты векторов BA и BC;
2) модули векторов BA и BC;
3) координаты вектора MP = 4BA – BC;
4) скалярное произведение векторов BA и BC;
5) косинус угла между векторами BA и BC.
ОТВЕТЫ: 1) BА (2; –1); BC (–2; 2);
2) |BA| = √[4+1] = √5; |BC| = √[4+4] = 2√2;
3) MP = 4BA – BC = (8+2; –4–2) = (10; –6);
4) BA • BC = 2 • (–2) + (–1) • 2 = –6;
5) cos a = (BA • BC) / (|BA| • |BC|) = –6 / (√5 • 2√2) = –0,94868 (а = 161,6°).
№ 2. Начертите треугольник ABC. Постройте вектор:
1) CA + AB; 2) BC – BA; 3) BA + BC.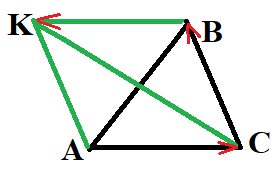
ОТВЕТ: 1) CA + AB = CB; 2) BC – BA = AC; 3) BA + BC = BK.
№ 3. Даны векторы m (2; p) и n (9; –3). При каком значении p векторы m и n: 1) коллинеарны; 2) перпендикулярны?
ОТВЕТ: 1) p = –2/3; 2) p = 6.
№ 4. На сторонах AB и AD параллелограмма ABCD отмечены соответственно точки E и F так, что AE : EB = 7 : 2, AF : FD = 5 : 1. Выразите вектор EF через векторы CD = а и CB = b .
ОТВЕТ: EF = EA + AF = 7/9 • a – 5/6 • b.
№ 5. Найдите косинус угла между векторами b = 6m – n и c = m + 3n, если m ⊥ n и |m| = |n| = 1.
ОТВЕТ: cos ∠(b, c) = 3/√370 = 3√370/370 (≈0,156).
ОТВЕТЫ на Вариант 4
№ 1. Даны точки A (1; 5), B (–3; 2) и C (2; 3). Найдите:
1) координаты векторов CA и CB;
2) модули векторов CA и CB;
3) координаты вектора DM = 3CA – 4CB;
4) скалярное произведение векторов CA и CB;
5) косинус угла между векторами CA и CB.
ОТВЕТЫ: 1) CА (–1; 2); CB (–5; –1);
2) |CA| = √[1+4] = √5; |CB| = √[25+1] = √26;
3) DM = 3CA – 4CB = (–3+20; 6+4) = (17; 10);
4) CA • CB = (–1) • (–5) + 2 • (–1) = 3;
5) cos a = (CA • CB) / (|CA| • |CB|) = 3 / (√5 • √26) = 0,263 (а = 74,74°).
№ 2. Начертите треугольник DEF. Постройте вектор:
1) DE + EF; 2) ED – EF; 3) FE + FD.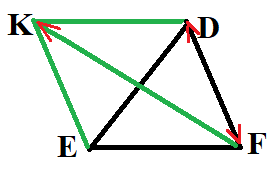
ОТВЕТ: 1) DE + EF = DF; 2) ED – EF = FD; 3) FE + FD = FK.
№ 3. Даны векторы а (x; 10) и b (–5; 4). При каком значении x векторы а и b: 1) коллинеарны; 2) перпендикулярны?
ОТВЕТ: 1) x = –12,5; 2) x = 8.
№ 4. На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS : SD = 5 : 3, CT : TD = 2 : 1. Выразите вектор ST через векторы BA = а и BC = b.
ОТВЕТ: ST = SD + DT = 3/8 • b – 1/3 • a.
№ 5. Найдите косинус угла между векторами m = 3а – b и n = a + 4b, если а ⊥ b и |a| = |b| = 1.
ОТВЕТ: cos ∠(m, n) = –1/(5√2) = –√2/10 (≈ –0,41).
Вернуться к Списку контрольных по 4 варианта
Посмотреть такую же контрольную из Методички (2 варианта)
Вы смотрели: Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Цитаты из пособия «Геометрия 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.





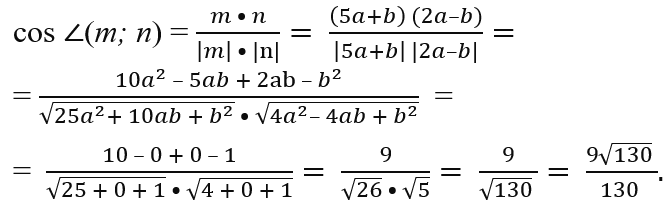
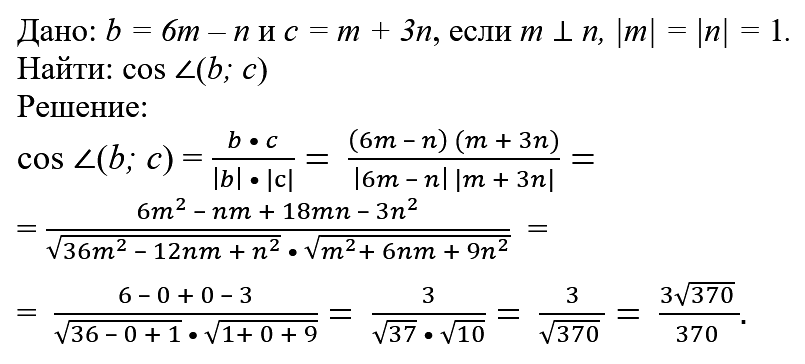
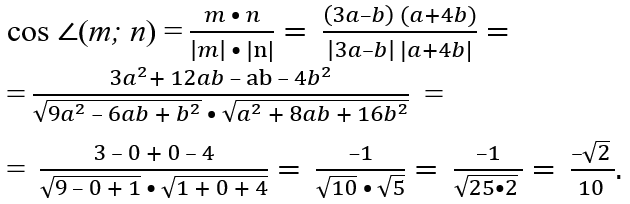
почему не приложены ответы?
согласна
В данном пособии ответов нет. В будущем постараемся найти и опубликовать.
ответы ждём
А можете сегодня добавить ответы, у нас завтра контрошка
Добавили ответы
а можете решения скинуть? очень надо!
добавьте, пожалуйста, хотя бы письменный ответ на задание 3,4,5 в 1 варианте, чтобы понимать, как решать
Добавили.
Даны векторы а (3; – 4) и b (m; 9). При каком значении m векторы а и b: 1) коллинеарны; 2) перпендикулярны?
2) Там мы 3*(-4)+9m=0
9m=12
m=12/9
Как вышло 12?
2) 3 * m + 9 * (-4) = 0
3m = 36 =>> m = 12.
вектора жестко в 8 классе проходят же?
Здравствуйте! Можно пожалуйста подробно решение на 5 задание в 3 варианте. Завтра кр. Спасите
Здраствуйте.
в 1 варианте в 5 задании в решении уравнения cos угла(a;b) в знаменателе есть |4m-p| * |m+2p| . Как из него дальше в знаменателе получилось √16m^2-8mp+p^2 * √m^2+4pm+4p^2 ?
|4m – p| = √[(4m – p)^2]
во 2 варианте в пятом задании мой ответ 9/√130. Решал по принципу 5 задания в 1 варианте, всё перепроверил, никак не смог получить 3/4. Помогите пожалуйста или перепроверьте 5 задание во 2 варианте
Исправлено.