Геометрия 8 Контрольная 3 (Мерзляк) с ответами. Контрольная работа по геометрии в 8 классе «Теорема Фалеса. Подобие треугольников» для УМК Мерзляк, Полонский, Якир из 4-х вариантов. Методическое пособие для родителей.
Геометрия 8 класс (УМК Мерзляк)
Контрольная № 3
Тема: Теорема Фалеса. Подобие треугольников
К-3 Вариант 1 (задания)
К-3 Вариант 2 (задания)
Нажмите на спойлер, чтобы увидеть ЗАДАНИЯ
К-3 Вариант 3 (задания)
Нажмите на спойлер, чтобы увидеть ЗАДАНИЯ
К-3 Вариант 4 (задания)
Нажмите на спойлер, чтобы увидеть ЗАДАНИЯ
Ответы на контрольную работу № 3
Решения и ОТВЕТЫ на Вариант 1
№ 1. На рисунке 15 MO || NP, OP = 20 см, PK = 8 см, MN = 15 см. Найдите отрезок NK.
Решение: по т-ме Фалеса OP/PK = MN/NK.
NK = PK*MN/OP = 8*15/20 = 6 (см).
ОТВЕТ: 6 см.
№ 2. Треугольники ABC и A1B1C1 подобны, причём сторонам AB и AC соответствуют стороны A1B1 и A1C1. Найдите неизвестные стороны этих треугольников, если AB = 12 см, AC = 18 см, A1C1 = 12 см, B1C1 = 18 см.
ОТВЕТ: А1В1 = 8 см, ВС = 27 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 3. Отрезок BM – биссектриса треугольника ABC, AB = 30 см, AM = 12 см, MC = 14 см. Найдите сторону BC.
Решение: воспользуемся свойством биссектрисы. Биссектриса внутреннего угла треугольника делит сторону, к которой она проведена, на части, пропорциональные прилежащим сторонам. Так как, по условию, ВМ — биссектриса угла АВС, то она делит, строну АС на отрезки, пропорциональные прилегающим сторонам:
АМ / АВ = СМ / ВС;
ВС = АВ * СМ / АМ = 30 * 14 / 12 = 35 (см).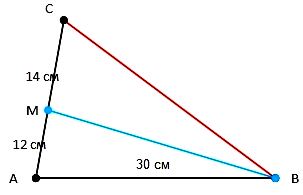
ОТВЕТ: 35 см.
№ 4. На стороне AB треугольника ABC отметили точку D так, что AD : BD = 5 : 3. Через точку D провели прямую, которая параллельна стороне AC треугольника и пересекает сторону BC в точке E. Найдите отрезок DE, если AC = 16 см.
Решение: ΔАВС подобен ΔDВЕ по 1 признаку подобия.
Следовательно, DE/AC = DB/AB = 3/(5+3);
DE = 16 • (3/8) = 6 (см).
ОТВЕТ: 6 см.
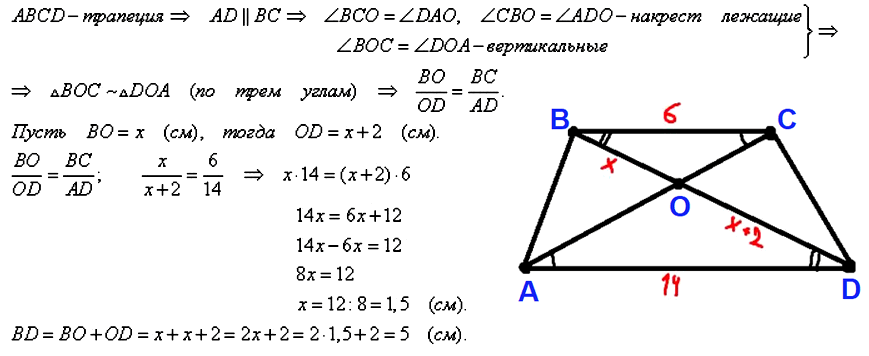
№ 5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, BC = 6 см, AD = 14 см, а отрезок BO на 2 см меньше отрезка OD. Найдите диагональ BD трапеции.
ОТВЕТ: 5 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 6. Через точку A, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка A делит на отрезки, длины которых относятся как 2 : 3. Найдите длину этой хорды.
ОТВЕТ: 20 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Расстояние между точками О и А : ОA = 5 (дано).
Хорда BC = BA + AC или BC = 2х + 3х = 5х (дано).
Радиус DO = OE = 11 (дано).
DA = DO + OA или DA = 16см.
АЕ = ОЕ — ОА или АЕ = 6см.
По свойству пересекающихся хорд DA * AE = 2x * 3x или
(DO + OA) * AE = 6x² или 16 * 6 = 6x².
Отсюда x = 4см и хорда ВС = 4 * 5 = 20см.
ОТВЕТЫ на Вариант 2
№ 1. На рисунке 16 EF || DC, AE = 40 см, AF = 24 см, FC = 9 см. Найдите отрезок ED.
ОТВЕТ: 15 см.
Краткое решение: по т-ме Фалеса ED/AE = FC/AF.
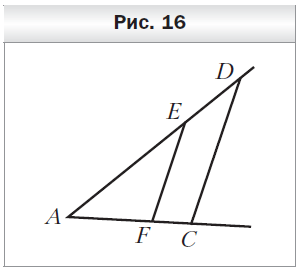ED = AE*FC/AF = 40*9/24 = 15 (см).
№ 2. Треугольники ABC и A1B1C1 подобны, причём сторонам AB и BC соответствуют стороны A1B1 и B1C1. Найдите неизвестные стороны этих треугольников, если BC = 22 см, AC = 14 см, B1C1 = 33 см, A1B1 = 15 см.
ОТВЕТ: АВ = 10 см, А1С1 = 21 см.
Краткое решение: Т. к. треугольники подобны, то отношения их сходственных сторон равны. Найдём отношение уже известных сторон: BC/B1C1 = 22/33 = 2/3;
Тогда AB/A1B1 = 2/3;
AB/15 = 2/3 => AB = 15/3•2 = 10 (см).
AC/A1C1 = 2/3;
14/A1C1 = 2/3 => A1C1 = 14/2•3 = 21 (см).
№ 3. Отрезок AE – биссектриса треугольника ABC, AB = 32 см, AC = 16 см, CE = 6 см. Найдите отрезок BE.
ОТВЕТ: 12 см.
Краткое решение: По свойству биссектрисы: делит сторону и угол пополам, делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Из этого следует: ВЕ = (ЕС*АВ)\АС = (6*32)\16 = 12 (см).
№ 4. На стороне AC треугольника ABC отметили точку E так, что AE : CE = 2 : 7. Через точку E провели прямую, которая параллельна стороне AB треугольника и пересекает сторону BC в точке F. Найдите сторону AB, если EF = 21 см.
ОТВЕТ: 27 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, AO = 10 см, OC = 4 см. Найдите основания трапеции, если их сумма равна 42 см.
ОТВЕТ: 12 см, 30 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
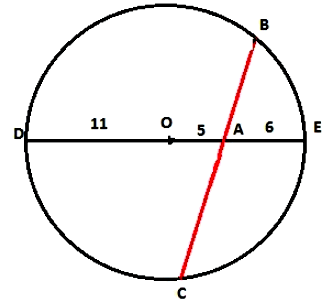
№ 6. Через точку B, лежащую внутри окружности, проведена хорда, которая делится точкой B на отрезки длиной 8 см и 12 см. Найдите радиус окружности, если точка B удалена от её центра на 5 см.
ОТВЕТ: 11 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Если хорды пересекаются, то произведения их отрезков, на которые их разделила точка пересечения, равны (св–во пересекающихся хорд): AB • BC = DB • BE
8 • 12 = (DO + OB) • BE, при этом DO = OB + BE = r
Пусть BE – это x, тогда 8 • 12 = ((5 + x) + 5) • x
96 = (x + 10) • x
x2 + 10x – 96 = 0
D = 100 + 384 = 484
x = (–10 + 22)/2 = 6 (см)
r = OB + BE = 5 + 6 = 11 (см)
ОТВЕТЫ на Вариант 3
№ 1. На рисунке 17 CF || BE, AE = 6 см, EF = 14 см, BC = 35 см. Найдите отрезок AB.
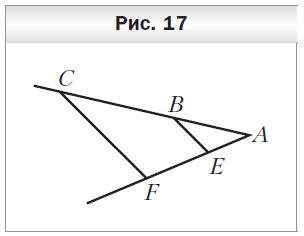ОТВЕТ: 15 см.
№ 2. Треугольники ABC и A1B1C1 подобны, причём сторонам AC и BC соответствуют стороны A1C1 и B1C1. Найдите неизвестные стороны этих треугольников, если AC = 28 см, AB = 49 см, B1C1 = 24 см, A1C1 = 16 см.
ОТВЕТ: А1В1 = 28 см, ВС = 42 см.
Краткое решение: Так как ΔАВС ~ ΔА1В1С1, то
AC : А1С1 = ВС : В1С1 = АВ : А1В1
28 : 16 = ВС : 24 ⇒ ВС = 28 × 24 ÷ 16 = 42 (см)
28 : 16 = 49 : А1В1
А1В1 = 16×49÷28 = 28 (см).
№ 3. Отрезок CK – биссектриса треугольника ABC, AC = 45 см, AK = 18 см, BK = 10 см. Найдите сторону BC.
ОТВЕТ: 25 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 4. На стороне AB треугольника ABC отметили точку M так, что AM : MB = 4 : 9. Через точку M провели прямую, которая параллельна стороне BC треугольника и пересекает сторону AC в точке K. Найдите отрезок MK, если BC = 26 см.
ОТВЕТ: 8 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, BO = 15 см, OD = 18 см, основание BC на 5 см меньше основания AD. Найдите основания трапеции.
ОТВЕТ: ВС = 25 см; AD = 30 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 6. Через точку C, находящуюся на расстоянии 11 см от центра окружности радиуса 13 см, проведена хорда, делящаяся точкой C на отрезки, длины которых относятся как 1 : 3. Найдите длину этой хорды.
ОТВЕТ: 16 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
ОТВЕТЫ на Вариант 4
№ 1. На рисунке 18 TP||SM, KP = 25 см, PM = 20 см, KT = 10 см. Найдите отрезок TS.
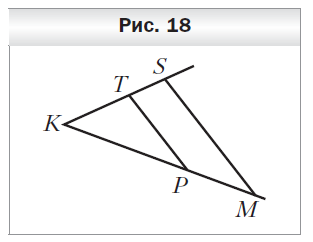ОТВЕТ: 8 см.
№ 2. Треугольники ABC и A1B1C1 подобны, причём сторонам AB и AC соответствуют стороны A1B1 и A1C1. Найдите неизвестные стороны этих треугольников, если AC = 9 см, BC = 27 см, B1C1 = 36 см, A1B1 = 28 см.
ОТВЕТ: АВ = 21 см, А1С1 = 12 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 3. Отрезок BD – биссектриса треугольника ABC, AB = 48 см, BC = 32 см, AD = 36 см. Найдите отрезок CD.
ОТВЕТ: 24 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 4. На стороне BC треугольника ABC отметили точку P так, что BP : PC = 5 : 6. Через точку P провели прямую, которая параллельна стороне AC треугольника и пересекает сторону AB в точке N. Найдите сторону AC, если PN = 15 см.
ОТВЕТ: 33 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, AO = 24 см, OC = 16 см, а отрезок OD на 9 см больше отрезка BO. Найдите диагональ BD трапеции.
ОТВЕТ: 45 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 6. Через точку D, лежащую внутри окружности, проведена хорда, которая делится точкой D на отрезки длиной 3 см и 4 см. Найдите расстояние от точки D до центра окружности, если радиус окружности равен 4 см.
ОТВЕТ: 2 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вы смотрели: Геометрия 8 Контрольная 3 (Мерзляк). Контрольная работа по геометрии в 8 классе «Теорема Фалеса. Подобие треугольников» для УМК Мерзляк, Полонский, Якир в 4-х вариантах. Методическое пособие.
Смотреть аналогичную контрольную № 3 с решениями (2 варианта)
Вернуться к Списку контрольных работ из Методички (по 4 варианта)
Списать получилось?
ага
Я вас прошу можете сделать решение! ко 2 контрольной
к КР-2 даны решения всех заданий варианта 1
вы гении там есть показать решение там смотрите
А у меня вопрос, как треугольники подобны по трём углам? Разве такой признак подобия треугольников есть и какой интересно же? У нас в учебниках только по двум углам.
Это не признак подобия, а определение. Подобные треугольники — это треугольники, у которых все три угла равны.
где решения?
Называйте номер задания и вариант, постараемся добавить решение. Полностью готовых на все задания пока нет.
можно пожалуйста решение к 6 заданию 2 варианта
Добавили решение.
Здравствуйте. Пожалуйста можете добавить подробное решение как и в первом варианте..остальным вариантаи
Сделайте решения не 3 вариант 3-4заданий и 4 вариант 3-4 задания
Добавили.